题目内容
13.△ABC是边长为2的等边三角形,$A\vec B•A\vec C$=2.分析 由题意可得$|\overrightarrow{AB}|=|\overrightarrow{AC}|=2$,<$\overrightarrow{AB},\overrightarrow{AC}$>=$\frac{π}{3}$,代入数量积公式得答案.
解答 解:如图,
$|\overrightarrow{AB}|=|\overrightarrow{AC}|=2$,<$\overrightarrow{AB},\overrightarrow{AC}$>=$\frac{π}{3}$,
∴$A\vec B•A\vec C$=|$\overrightarrow{AB}$||$\overrightarrow{AC}$|•cos$\frac{π}{3}$=2×2×$\frac{1}{2}=2$.
故答案为:2.
点评 本题考查平面向量的数量积运算,是基础的计算题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
1.椭圆$\frac{x^2}{9}+\frac{y^2}{2}=1$的焦点为F1,F2,点P在椭圆上,若|PF1|=2,则∠F1PF2=( )
| A. | 30o | B. | 60o | C. | 120o | D. | 150o |
8.在△ABC中,A=30°,则$\sqrt{3}sinA-cos({B+C})$的值为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2 |
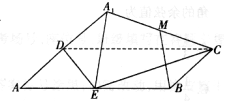 如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中:
如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中: