题目内容
2.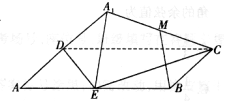 如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中:
如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中:①|BM|是定值;
②点M在某个球面上运动;
③存在某个位置,使DE⊥A1C;
④存在某个位置,使MB∥平面A1DE.
其中正确的命题是①②④.
分析 取A1D的中点N,连结MN,EN,则可证明四边形MNEB是平行四边形,从而BM$\stackrel{∥}{=}$EN,于是BM∥平面A1DE,从而可判断①②④一定成立,假设③成立,则可推出DE⊥A1E,得出矛盾.
解答  解:取A1D的中点N,连结MN,EN,
解:取A1D的中点N,连结MN,EN,
则MN为△A1CD的中位线,∴MN$\stackrel{∥}{=}$$\frac{1}{2}$CD,
∵E是矩形ABCD的边AB的中点,∴BE$\stackrel{∥}{=}$$\frac{1}{2}$CD,
∴MN$\stackrel{∥}{=}$BE,
∴四边形MNEB是平行四边形,
∴BM$\stackrel{∥}{=}$EN,
∴BM为定值,M在以B为球心,以BM为半径的球面上,故①正确,②正确;
又NE?平面A1DE,BM?平面A1DE,
∴BM∥平面A1DE,故④正确;
由勾股定理可得DE=CE=2$\sqrt{2}$,∴DE2+CE2=CD2,
∴DE⊥CE,若DE⊥A1C,又A1C∩CE=C,
∴DE⊥平面A1CE,又A1E?平面A1CE,
∴DE⊥A1E,而这与∠AED=45°矛盾.故③错误.
故答案为:①②④.
点评 本题考查了空间线面位置关系的判断,属于中档题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
10.已知$sinα+cosα=\frac{1}{5}$,且$-\frac{π}{2}≤α≤\frac{π}{2}$,那么tanα等于( )
| A. | $-\frac{4}{3}$ | B. | $-\frac{3}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
17.已知椭圆x2+4y2=1的长轴长为( )
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
7.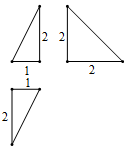 已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线的成角余弦值为( )
已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线的成角余弦值为( )
 已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线的成角余弦值为( )
已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线的成角余弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
11.设集合M={x|x2>4},N={x|x<3},则以下各式正确的是( )
| A. | M∪N={x|x<3} | B. | M∩N={x|2<|x|<3} | C. | M∩N={x|2<x<3} | D. | M∪N=R |
 如图,等腰三角形ABC中,∠B=∠C,D在BC上,∠BAD大小为α,∠CAD大小为β.
如图,等腰三角形ABC中,∠B=∠C,D在BC上,∠BAD大小为α,∠CAD大小为β.