题目内容
将直线2x-y+λ=0沿x轴向右平移1个单位,所得直线与圆x2+y2+2x-4y=0相切,则实数λ的值为( )
| A、-3或7 | B、-2或8 |
| C、0或10 | D、1或11 |
考点:圆的切线方程
专题:计算题,直线与圆
分析:根据直线平移的规律,由直线2x-y+λ=0沿x轴向左平移1个单位得到平移后直线的方程,然后因为此直线与圆相切得到圆心到直线的距离等于半径,利用点到直线的距离公式列出关于λ的方程,求出方程的解即可得到λ的值.
解答:
解:把圆的方程化为标准式方程得(x+1)2+(y-2)2=5,圆心坐标为(-1,2),半径为
,
直线2x-y+λ=0沿x轴向左平移1个单位后所得的直线方程为2(x+1)-y+λ=0,
因为该直线与圆相切,则圆心(-1,2)到直线的距离d=
=r=
,
化简得|λ-2|=5,即λ-2=5或λ-2=-5,
解得λ=-3或7
故选A.
| 5 |
直线2x-y+λ=0沿x轴向左平移1个单位后所得的直线方程为2(x+1)-y+λ=0,
因为该直线与圆相切,则圆心(-1,2)到直线的距离d=
| |λ-2| | ||
|
| 5 |
化简得|λ-2|=5,即λ-2=5或λ-2=-5,
解得λ=-3或7
故选A.
点评:本题考查圆的方程,考查直线与圆的位置关系,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
在△ABC中,AB=4,BC=3,∠ABC=90°,若使△ABC绕直线BC旋转一周,则所形成的几何体的体积是( )
| A、36π | B、28π |
| C、20π | D、16π |
设α∈{-1,1,
,2,3},则使函数y=xα为奇函数α值的个数为( )
| 1 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
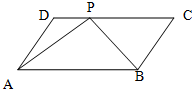 如图,在四边形ABCD中,
如图,在四边形ABCD中,