题目内容
3.m∈R,函数f(x)=mx-lnx+1.(1)讨论函数f(x)的单调区间和极值;
(2)将函数f(x)的图象向下平移1个单位后得到g(x)的图象,且x1=$\sqrt{e}$(e为自然对数的底数)和x2是函数g(x)的两个不同的零点,求m的值并证明:x2>e$\sqrt{e}$.
分析 (1)求出函数f(x)的定义域,求导数,通过f′(x)=0,得x=1,利用导函数的符号,推出函数的单调区间.
(2)利用g(x)=mx-lnx,且x1=$\sqrt{e}$是函数g(x)的零点,推出m值,利用函数的零点判定定理,结合函数g(x)在(2$\sqrt{e}$,+∞)上单调递增,求解即可.
解答 (1)函数f(x)的定义域为(0,+∞).求导得f′(x)=m-$\frac{1}{x}$=$\frac{mx-1}{x}$.
①若m≤0,则f′(x)<0,f(x)是(0,+∞)上的减函数,无极值; …(2分)
②若m>0,令f′(x)=0,得x=$\frac{1}{m}$.…(3分)
当x∈(0,$\frac{1}{m}$)时,f′(x)<0,f(x)是减函数;
当x∈($\frac{1}{m}$,+∞)时,f′(x)>0,f(x)是增函数.…(5分)
所以当x=$\frac{1}{m}$时,f(x)有极小值,极小值为f($\frac{1}{m}$)=2-ln$\frac{1}{m}$=2+lnm.
综上所述,当m≤0时,f(x)的递减区间为(0,+∞),无极值;
当m>0时,f(x)的递增区间为($\frac{1}{m}$,+∞),递减区间为(0,$\frac{1}{m}$),极小值为2+lnm.…(6分)
(2)证明:因为g(x)=mx-lnx,且x1=$\sqrt{e}$是函数g(x)的零点,
所以g($\sqrt{e}$)=0,即m$\sqrt{e}$-$\frac{1}{2}$=0,解得m=$\frac{1}{{2\sqrt{e}}}=\frac{{\sqrt{e}}}{2e}$.…(8分)
所以g(x)=$\frac{1}{{2\sqrt{e}}}x$-lnx.因为g(${e}^{\frac{3}{2}}$)=$\frac{e}{2}$-$\frac{3}{2}$<0,g(${e}^{\frac{5}{2}}$)=$\frac{e^2}{2}$-$\frac{5}{2}$>0,
所以g(${e}^{\frac{3}{2}}$)g(${e}^{\frac{5}{2}}$)<0.….(10分)
由(1)知,函数g(x)在(2$\sqrt{e}$,+∞)上单调递增,
所以函数g (x)在区间(${e}^{\frac{3}{2}}$,${e}^{\frac{5}{2}}$)上有唯一零点,因此x2>${e}^{\frac{3}{2}}$,即x2>$e\sqrt{e}$….(12分)
注:其它解法酌情给分.
点评 本题考查函数的导数的应用,函数的单调性以及函数的极值,零点判定定理的应用,考查分析问题解决问题的能力.

 阅读快车系列答案
阅读快车系列答案| A. | $-\sqrt{2}$ | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | 4 |
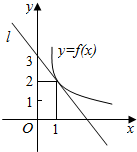 如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,令h(x)=xf(x),h′(x)是h(x)的导函数,则h′(1)的值是( )
如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,令h(x)=xf(x),h′(x)是h(x)的导函数,则h′(1)的值是( )| A. | 2 | B. | 1 | C. | -1 | D. | $\frac{1}{2}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | c>a>b | B. | c>b>a | C. | a>b>c | D. | b>a>c |