题目内容

在直角坐标平面内，将每个点绕原点按逆时针方向旋转45°的变换R所对应的矩阵为M，将每个点横、纵坐标分别变为原来的
2
倍的变换T所对应的矩阵为N．
（Ⅰ）求矩阵M的逆矩阵M-1；
（Ⅱ）求曲线xy=1先在变换R作用下，然后在变换T作用下得到的曲线方程．
考点：几种特殊的矩阵变换
专题：选作题,矩阵和变换
分析：（Ⅰ）求出M=
2
2
-
2
2
2
2
2
2
，|M|=1，即可求矩阵M的逆矩阵M-1；    
（Ⅱ）求出NM，可得坐标之间的关系，代人方程xy=1整理，即可求曲线C′的方程．
解答： 解：（Ⅰ）∵M=
2
2
-
2
2
2
2
2
2
，|M|=1，
∴M-1=
2
2
2
2
-
2
2
2
2
．
（Ⅱ）∵N=
2
0
0
2
，M=
2
2
-
2
2
2
2
2
2

∴矩阵NM=
1-1
11
，它所对应的变换为
x′=x-y
y′=x+y

解得
x=
x′+y′
2
y=
-x′+y′
2

把它代人方程xy=1整理，得（y′）2-（x′）2=4，
即经过矩阵MN变换后的曲线C′方程为y2-x2=4．
点评：本题给出矩阵变换，求曲线C在矩阵M对应变换作用下得到的曲线C'方程，着重考查了矩阵与变换的运算、曲线方程的求法等知识，属于中档题．
练习册系列答案
相关题目
试用tan
α
2
表示sinα，并证明．
已知数列{an}的前n项和为Sn，且a1=3，an=2Sn+1+3n（n∈N*，n≥2）．
（1）求证：数列{
Sn
3n
}是等差数列；
（2）求数列{an}的通项公式；
（3）令bn=
2n2-5n-3
an
，如果对任意n∈N*，都有bn+
2
9
t＜t2成立，求实数t的取值范围．
在（2x+
1
x2
）n的展开式中，第三项的二项式系数比第二项的二项式系数大27，求展开式中的常数项及系数最大的项．
已知直线a∥b，直线l与a、b都相交，求证：过a、b、l有且只有一个平面．
已知等比数列an的公比为q＞1，又a172=a24，求使a1+a2+…+an＞
1
a1
+
1
a2
+
1
a3
+…+
1
an
成立的自然数n的取值范围．
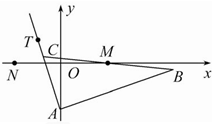已知△ABC的边AB所在直线的方程为x-3y-6=0，M（2，0）满足
BM
=
MC
，点T（-1，1）在AC边所在直线上且满足
AT
•
AB
=0．
（1）求AC边所在直线的方程．
（2）求△ABC外接圆的方程．
若一个棱锥的底面是正多边形，并且顶点在底面的射影是底面的中心，这样的棱锥叫做正棱锥．已知一个正六棱锥的各个顶点都在半径为3的球面上，则该正六棱锥的体积的最大值为
 
．
若圆C的圆心为（1，1），经过原点，则其方程为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网