题目内容
已知等比数列an的公比为q＞1，又a172=a24，求使a1+a2+…+an＞
+
+
+…+
成立的自然数n的取值范围．
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
考点：数列与不等式的综合
专题：综合题,等差数列与等比数列
分析：求出数列的前n项和，根据不等式之间的关系即可得到结论．
解答：
解：设首项为a1，公比为q，依题意有（a1q16）2=a1q23，
∴a1q9=1．则a1＞0，且a1=q-9，
∵{an}为等比数列，∴{
}是以
为首项，
为公比的等比数列．
则不等式等价为
＞
，
∵q＞1，把a1=q-9，即a12=q-18代入整理，
得q-18（1-qn）＞q1-n（1-qn），
∴q-18＞q1-n，
∴-18＜1-n，
即n＜19，
∵n∈N*，∴1≤n≤18，n∈N*．
∴a1q9=1．则a1＞0，且a1=q-9，
∵{an}为等比数列，∴{
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| q |
则不等式等价为
| a1(1-qn) |
| 1-q |
| ||||
1-
|
∵q＞1，把a1=q-9，即a12=q-18代入整理，
得q-18（1-qn）＞q1-n（1-qn），
∴q-18＞q1-n，
∴-18＜1-n，
即n＜19，
∵n∈N*，∴1≤n≤18，n∈N*．
点评：本题主要考查等比数列的通项公式和前n项和的应用，考查数列与不等式的应用，综合性较强，运算量较大．
练习册系列答案
相关题目
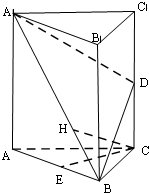如图，在三棱柱ABC-A1B1C1中，△ABC是边长为2的等边三角形，AA1⊥平面ABC，D，E分别是CC1，AB的中点．