题目内容
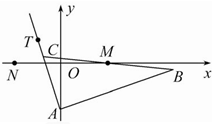 已知△ABC的边AB所在直线的方程为x-3y-6=0,M(2,0)满足
已知△ABC的边AB所在直线的方程为x-3y-6=0,M(2,0)满足| BM |
| MC |
| AT |
| AB |
(1)求AC边所在直线的方程.
(2)求△ABC外接圆的方程.
考点:直线的一般式方程与直线的性质
专题:直线与圆
分析:(1)利用相互垂直的正弦斜率之间的关系可得直线AC的斜率,再利用点斜式即可得出;
(2)利用直角三角形的外接圆的性质可知:斜边的中点即为外接圆的圆心,求出交点A的坐标,再利用两点之间的距离公式即可得出半径.
(2)利用直角三角形的外接圆的性质可知:斜边的中点即为外接圆的圆心,求出交点A的坐标,再利用两点之间的距离公式即可得出半径.
解答:
解:(1)∵
•
=0,
∴AT⊥AB,又T在AC上,
∴AC⊥AB,△ABC为直角三角形,
又AB边所在直线的方程为x-3y-6=0,
∴直线AC的斜率为-3.
又∵点T(-1,1)在直线AC上,
∴AC边所在直线的方程为y-1=-3(x+1),即3x+y+2=0.
(2)AC与AB的交点为A,
∴由
,解得点A的坐标为(0,-2),
∵
=
,
∴M(2,0)为Rt△ABC斜边上的中点,即为Rt△ABC外接圆的圆心,
又r=|AM|=
=2
.
从而△ABC外接圆的方程为(x-2)2+y2=8.
| AT |
| AB |
∴AT⊥AB,又T在AC上,
∴AC⊥AB,△ABC为直角三角形,
又AB边所在直线的方程为x-3y-6=0,
∴直线AC的斜率为-3.
又∵点T(-1,1)在直线AC上,
∴AC边所在直线的方程为y-1=-3(x+1),即3x+y+2=0.
(2)AC与AB的交点为A,
∴由
|
∵
| BM |
| MC |
∴M(2,0)为Rt△ABC斜边上的中点,即为Rt△ABC外接圆的圆心,
又r=|AM|=
| (2-0)2+(0+2)2 |
| 2 |
从而△ABC外接圆的方程为(x-2)2+y2=8.
点评:本题考查了相互垂直的正弦斜率之间的关系、点斜式、直角三角形的外接圆的性质、直线的交点、两点之间的距离公式等基础知识与基本技能方法,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
 如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.
如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.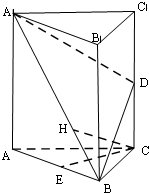 如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E分别是CC1,AB的中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E分别是CC1,AB的中点.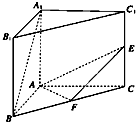 设在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=90°,E,F依次为C1C,BC的中点.则异面直线A1B、EF所成角θ的大小
设在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=90°,E,F依次为C1C,BC的中点.则异面直线A1B、EF所成角θ的大小