题目内容
若一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥.已知一个正六棱锥的各个顶点都在半径为3的球面上,则该正六棱锥的体积的最大值为 .
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:设球心到底面的距离为x,则底面边长为
,高为x+3,表示出体积,利用导数求最值,即可得出结论.
| 9-x2 |
解答:
解:设球心到底面的距离为x,则底面边长为
,高为x+3,则
V=
•
(9-x2)•6(x+3)=
(-x3-3x2+9x+27),其中0<x<3,
V′=0,可得x2+2x-3=0,解得x=1或x=-3(舍去)
∴Vmax=V(1)=
(-1-3+9+27)=16
.
故答案为:16
.
| 9-x2 |
V=
| 1 |
| 3 |
| ||
| 4 |
| ||
| 2 |
V′=0,可得x2+2x-3=0,解得x=1或x=-3(舍去)
∴Vmax=V(1)=
| ||
| 2 |
| 3 |
故答案为:16
| 3 |
点评:本题考查棱柱、棱锥、棱台的体积,考查导数知识的运用,确定体积的表达式是关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
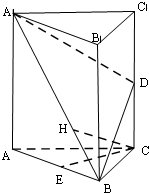 如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E分别是CC1,AB的中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E分别是CC1,AB的中点.