题目内容
己知命题p:方程
+
=1表示焦点在y轴的双曲线;命题q:关于x的不等式x2-2x+m>0的解集是R;
若“p∧q”是假命题,“p∨q”是真命题,求实数m的取值范围.
| x2 |
| m-4 |
| y2 |
| m-2 |
若“p∧q”是假命题,“p∨q”是真命题,求实数m的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:本题考查的知识点是复合命题的真假判定,解决的办法是先判断组成复合命题的简单命题的真假,再根据真值表进行判断.
解答:
∵命题p:方程
+
=1表示焦点在y轴的双曲线
∴当命题p为真命题时,
,
∴解得实数m的取值范围,2<m<4
又∵命题q:关于x的不等式x2-2x+m>0的解集是R
∴当命题q为真命题时,△=4-4m<0
∴解得实数m的取值范围m>1
∵若“p∧q”是假命题,“p∨q”是真命题
∴p、q一个是假命题,一个是真命题
①当p是真命题,q是假命题时
成立,解得m∈φ
②当q是真命题,p是假命题时
成立,解得1<m≤2或m≥4
综合上述,得实数m的取值范围:1<m≤2或m≥4
| x2 |
| m-4 |
| y2 |
| m-2 |
∴当命题p为真命题时,
|
∴解得实数m的取值范围,2<m<4
又∵命题q:关于x的不等式x2-2x+m>0的解集是R
∴当命题q为真命题时,△=4-4m<0
∴解得实数m的取值范围m>1
∵若“p∧q”是假命题,“p∨q”是真命题
∴p、q一个是假命题,一个是真命题
①当p是真命题,q是假命题时
|
②当q是真命题,p是假命题时
|
综合上述,得实数m的取值范围:1<m≤2或m≥4
点评:本题考查的知识点是复合命题的真假判定,属于基础题目

练习册系列答案
相关题目
若
=
,则tan2α=( )
| 1+cos2α |
| sin2α |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
下列表述正确的是( )
| A、0∈∅ | B、{0}∈∅ |
| C、{0}⊆∅ | D、∅⊆{0} |
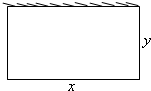 现要用一段长为l的篱笆围成一边靠墙的矩形菜园(如图所示),则围成的菜园最大面积是
现要用一段长为l的篱笆围成一边靠墙的矩形菜园(如图所示),则围成的菜园最大面积是 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AB∥DC,AB⊥BC,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AB∥DC,AB⊥BC,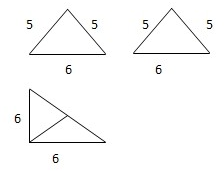 已知某三棱锥的三视图如表示,
已知某三棱锥的三视图如表示,