题目内容
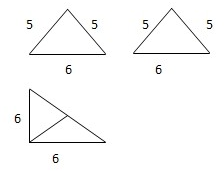 已知某三棱锥的三视图如表示,
已知某三棱锥的三视图如表示,(1)求此三棱锥的表面积和体积;
(2)求它的外接球的表面积.
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:(1)由三视图知几何体为三棱锥,且顶点在底面上的射影是底面直角三角形斜边的中点,侧面ABC与ABD的斜高为5,底面直角边长为6,求出AM,CD,代入面积公式计算;
(2)利用其直观图,设外接球的球心为O,OM=x,列方程4+x=
求出x,从而求出外接球的半径R,代入球的表面积函数计算.
(2)利用其直观图,设外接球的球心为O,OM=x,列方程4+x=
(3
|
解答:
解:(1)由三视图知几何体为三棱锥,且顶点在底面上的射影是底面直角三角形斜边的中点,
侧面ABC与ABD的斜高为5,底面直角边长为6,其直观图如图:
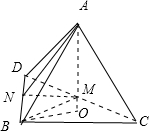
∴MN=3,AM=4,CD=6
,
∴三棱锥的表面积S=
×6×6+2×
×6×5+
×6
×4=48+12
;
三棱锥的体积V=
×
×6×6×4=24;
(2)∵BM=MC=MD=3
,且AM⊥平面BCD,设外接球的球心为O,OM=x,
则4+x=
⇒x=
,
∴球的半径R=4+
=
,
∴外接球的表面积为4π×(
)2=
π.
侧面ABC与ABD的斜高为5,底面直角边长为6,其直观图如图:

∴MN=3,AM=4,CD=6
| 2 |
∴三棱锥的表面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
三棱锥的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
(2)∵BM=MC=MD=3
| 2 |
则4+x=
(3
|
| 1 |
| 4 |
∴球的半径R=4+
| 1 |
| 4 |
| 17 |
| 4 |
∴外接球的表面积为4π×(
| 17 |
| 4 |
| 289 |
| 4 |
点评:本题考查了由三视图求几何体的表面积、体积,考查了接体的表面积,解题的关键是判断几何体的形状及三视图的数据所对应的几何量.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设a∈R,则“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”是“a=1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
平面四边形ABCD中,AD=AB=
,CD=CB=
,且AD⊥AB,现将△ABD沿着对角线BD翻折成△A′BD,则在△A′BD折起至转到平面BCD内的过程中,直线A′C与平面BCD所成的最大角的正切值为( )
| 2 |
| 5 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
已知△ABC外接圆的半径为1,圆心为O.若|
|=|
|,且2
+
+
=0,则
•
等于( )
| OA |
| AB |
| OA |
| AB |
| AC |
| CA |
| CB |
A、
| ||
B、2
| ||
C、
| ||
| D、3 |