题目内容
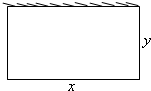现要用一段长为l的篱笆围成一边靠墙的矩形菜园（如图所示），则围成的菜园最大面积是考点：基本不等式
专题：不等式的解法及应用
分析：由题意可得：x+2y=l，x＞0，y＞0．利用基本不等式即可得出xy的最大值．
解答：
解：由题意可得：x+2y=l，x＞0，y＞0．
∴l≥2
，解得xy≤
，当且仅当x=2y=
时取等号．
∴S=xy≤
．
∴则围成的菜园最大面积是
．
故答案为：
．
∴l≥2
| 2xy |
| l2 |
| 8 |
| l |
| 2 |
∴S=xy≤
| l2 |
| 8 |
∴则围成的菜园最大面积是
| l2 |
| 8 |
故答案为：
| l2 |
| 8 |
点评：本题考查了基本不等式的性质和矩形的面积，属于基础题．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
设x是实数，且满足等式
+
=cosθ，则实数θ等于（以下各式中k∈Z）（ ）
| x |
| 2 |
| 1 |
| 2x |
| A、2kπ | ||
| B、（2k+1）π | ||
| C、kπ | ||
D、kπ+
|
已知α，β是方程x2+ax+2b=0的两根，且α∈[0，1]，β∈[1，2]，a∈R，b∈R，求
的最大值与最小值之和为（ ）
| b-3 |
| a-3 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
设f（x）=e|x|，则
f（x）dx=（ ）
| ∫ | 4 -2 |
| A、e4-e2 |
| B、e4+e2 |
| C、-e4+e2+2 |
| D、e4+e2-2 |