题目内容
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC=| 1 |
| 2 |
| PE |
| EB |
(1)当λ=2时,求证:PD∥面EAC;
(2)若直线PA与平面EAC所成角为30°,求实数λ的值.
考点:用空间向量求直线与平面的夹角,直线与平面平行的判定,直线与平面所成的角
专题:空间位置关系与距离,空间向量及应用
分析:(1)由已知条件,推导出EM∥PD,利用直线与平面平行的判定定理能证明PD∥面EAC.
(2)以A为坐标原点,分别以AB,AP为y轴,Z轴建立空间直角坐标系,利用向量法能求出实数λ的值.
(2)以A为坐标原点,分别以AB,AP为y轴,Z轴建立空间直角坐标系,利用向量法能求出实数λ的值.
解答:
(本小题满分为10分)
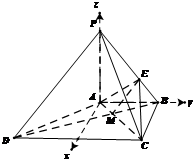 (1)证明:连接BD交AC于点M,连结ME,
(1)证明:连接BD交AC于点M,连结ME,
∵AB∥DC,∴
=
=
,
当λ=2时
=
,
∴
=
,∴EM∥PD.
∵PD不包含于平面EAC,EM?平面EAC
∴PD∥面EAC.…(4分)
(2)由已知可以A为坐标原点,分别以AB,AP为y轴,Z轴建立空间直角坐标系,
设DC=2,则A(0,0,0),C(1,1,0),B(0,1,0),P(0,0,1),
由
=λ
,得E点的坐标为(0,
,
)…(6分)
所以
=(1,1,0),
=(0,
,
).
设平面EAC的一个法向量为
=(x,y,z),
则
,
设z=λ,则y=-1,x=1,所以
=(1,-1,λ)…(8分)
若直线PA与平面EAC所成角为30°,
则cos60°=
,…(9分)
解得λ=
…(10分)
 (1)证明:连接BD交AC于点M,连结ME,
(1)证明:连接BD交AC于点M,连结ME,∵AB∥DC,∴
| |MB| |
| |MD| |
| |AB| |
| |CD| |
| 1 |
| 2 |
当λ=2时
| |BE| |
| |EP| |
| 1 |
| 2 |
∴
| |MB| |
| |MD| |
| |BE| |
| |EP| |
∵PD不包含于平面EAC,EM?平面EAC
∴PD∥面EAC.…(4分)
(2)由已知可以A为坐标原点,分别以AB,AP为y轴,Z轴建立空间直角坐标系,
设DC=2,则A(0,0,0),C(1,1,0),B(0,1,0),P(0,0,1),
由
| PE |
| EB |
| λ |
| 1+λ |
| 1 |
| 1+λ |
所以
| AC |
| AE |
| λ |
| 1+λ |
| 1 |
| 1+λ |
设平面EAC的一个法向量为
| n |
则
|
设z=λ,则y=-1,x=1,所以
| n |
若直线PA与平面EAC所成角为30°,
则cos60°=
| λ | ||
|
解得λ=
| ||
| 3 |
点评:本题考查直线与平面平行的证明,考查直线与平面所成角的应用,解题时要注意等价转化思想和向量法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知△ABC的顶点A(2,3),且三条中线交于点G(4,1),则BC边上的中点坐标为( )
| A、(5,0) |
| B、(6,-1) |
| C、(5,-3) |
| D、(6,-3) |
已知α,β是方程x2+ax+2b=0的两根,且α∈[0,1],β∈[1,2],a∈R,b∈R,求
的最大值与最小值之和为( )
| b-3 |
| a-3 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
设a∈R,则“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”是“a=1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于( )
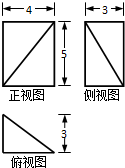

| A、10cm3 |
| B、20cm3 |
| C、30cm3 |
| D、40cm3 |