题目内容
已知一直线的倾斜角为α,且满足45°≤α≤150°,则直线的斜率的取值范围为( )
A、[-
| ||||
B、(-∞,-
| ||||
C、(-∞,-
| ||||
D、[-
|
考点:直线的倾斜角
专题:直线与圆
分析:利用倾斜角与斜率的关系即可得出.
解答:
解:∵满足45°≤α≤150°,
∴α≠90°时,k=tanα≥tan45°或k=tanα≤tan150°,
解得k≥1或k≤-
.
故选:B.
∴α≠90°时,k=tanα≥tan45°或k=tanα≤tan150°,
解得k≥1或k≤-
| ||
| 3 |
故选:B.
点评:本题考查了倾斜角与斜率的关系,属于基础题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
cos35°cos25°-sin35°sin25°的值为( )
A、
| ||
| B、cos10° | ||
C、-
| ||
| D、-cos10° |
函数f(x)=sinx-x,x∈[-
,
]值域是( )
| π |
| 2 |
| π |
| 2 |
A、[1-
| ||||
| B、[-1,0] | ||||
C、[1-
| ||||
D、[0,
|
(B题)下列说法中正确的是( )
| A、任何三个不共线的向量可构成空间向量的一个基底 |
| B、空间的基底有且仅有一个 |
| C、两两垂直的三个非零向量可构成空间的一个基底 |
| D、基底{a,b,c}中基向量与基底{e,f,g}中基向量对应相等 |
函数y=-
在x=
处的切线方程是( )
| 1 |
| x |
| 1 |
| 2 |
| A、y=4x |
| B、y=4x-4 |
| C、y=4(x+1) |
| D、y=2x-4 |
下列说法正确的是( )
A、向量
| ||||||||
B、向量
| ||||||||
C、向量
| ||||||||
| D、单位向量都相等 |
函数f(x)=mx2-2mx-4(m+5)在区间[0,4]内有零点,则实数m的取值范围( )
| A、[-4,0)∪(0,5] |
| B、(-∞,-4]∪[5,+∞) |
| C、[-4,5] |
| D、[-5,5] |
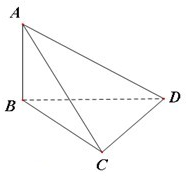 如图,AB⊥平面BCD,BD⊥CD,若AB=BC=2BD,则二面角B-AC-D的正弦值为
如图,AB⊥平面BCD,BD⊥CD,若AB=BC=2BD,则二面角B-AC-D的正弦值为