题目内容
函数y=sin(2x+
)(x∈[0,π])的单调递减区间是 .
| π |
| 3 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:对于函数y=sin(2x+
),令2kπ+
≤2x+
≤2kπ+
,k∈z,求得x的范围,再结合x∈[0,π],可得函数的单调递减区间.
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
解答:
解:对于函数y=sin(2x+
),令2kπ+
≤2x+
≤2kπ+
,k∈z,
求得kπ+
≤x≤kπ≤kπ+
,k∈z,
再结合x∈[0,π],可得函数的单调递减区间是[
,
],
故答案为:[
,
].
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
求得kπ+
| π |
| 12 |
| 7π |
| 6 |
再结合x∈[0,π],可得函数的单调递减区间是[
| π |
| 12 |
| 7π |
| 12 |
故答案为:[
| π |
| 12 |
| 7π |
| 12 |
点评:本题主要考查正弦函数的单调性,属于基础题.

练习册系列答案
相关题目
设函数f(x)=2cos(2x+
)-1,则( )
| π |
| 6 |
| A、函数f(x)的图象过点(0,0) | ||||
B、函数f(x)的图象关于x=
| ||||
C、函数f(x)在[-
| ||||
| D、函数f(x)最大值为2 |
函数y=-
在x=
处的切线方程是( )
| 1 |
| x |
| 1 |
| 2 |
| A、y=4x |
| B、y=4x-4 |
| C、y=4(x+1) |
| D、y=2x-4 |

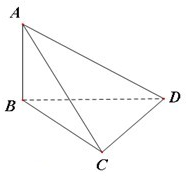 如图,AB⊥平面BCD,BD⊥CD,若AB=BC=2BD,则二面角B-AC-D的正弦值为
如图,AB⊥平面BCD,BD⊥CD,若AB=BC=2BD,则二面角B-AC-D的正弦值为