题目内容
若函数f(x)=a2-sinx,则f′(x)=( )
| A、-sinx |
| B、-cosx |
| C、2a+sinx |
| D、2a-sinx |
考点:导数的运算
专题:导数的概念及应用
分析:直接利用求导的法则求导即可.
解答:
解:因为函数f(x)=a2-sinx,
所以f′(x)=-cosx.
故选:B.
所以f′(x)=-cosx.
故选:B.
点评:本题考查简单函数的求导法则,属于基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
已知x,y满足x+2y=2,那么3x+9y的最小值是( )
| A、3 | B、6 | C、9 | D、不存在 |
设函数f(x)=2cos(2x+
)-1,则( )
| π |
| 6 |
| A、函数f(x)的图象过点(0,0) | ||||
B、函数f(x)的图象关于x=
| ||||
C、函数f(x)在[-
| ||||
| D、函数f(x)最大值为2 |
cos35°cos25°-sin35°sin25°的值为( )
A、
| ||
| B、cos10° | ||
C、-
| ||
| D、-cos10° |
函数f(x)=sinx-x,x∈[-
,
]值域是( )
| π |
| 2 |
| π |
| 2 |
A、[1-
| ||||
| B、[-1,0] | ||||
C、[1-
| ||||
D、[0,
|
函数f(x)=mx2-2mx-4(m+5)在区间[0,4]内有零点,则实数m的取值范围( )
| A、[-4,0)∪(0,5] |
| B、(-∞,-4]∪[5,+∞) |
| C、[-4,5] |
| D、[-5,5] |
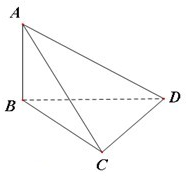 如图,AB⊥平面BCD,BD⊥CD,若AB=BC=2BD,则二面角B-AC-D的正弦值为
如图,AB⊥平面BCD,BD⊥CD,若AB=BC=2BD,则二面角B-AC-D的正弦值为