题目内容
有下列命题:
①到定点的距离等于到定直线的距离点的轨迹为抛物线;
②设集合M={x|0<x≤3},N={x|0<x≤2},则“a∈M”是“a∈N”的充分而不必要条件;
③曲线
+
=1表示双曲线;
④直线l过双曲线
-
=1的焦点截双曲线的弦长为2的直线仅有一条.
则上述命题中真命题为 (填上序号)
①到定点的距离等于到定直线的距离点的轨迹为抛物线;
②设集合M={x|0<x≤3},N={x|0<x≤2},则“a∈M”是“a∈N”的充分而不必要条件;
③曲线
| x2 |
| 2sinθ+3 |
| y2 |
| sinθ-2 |
④直线l过双曲线
| x2 |
| 4 |
| y2 |
| 2 |
则上述命题中真命题为
考点:命题的真假判断与应用
专题:简易逻辑
分析:对于①,根据抛物线的定义进行判断;
对于②利用两集合间的包含关系转化为充分、必要性的关系;
对于③利用双曲线的标准方程满足的条件判断,即在此题方程形式下,只需前后两个分母异号即可;
对于④先算出焦点弦的长,和2比较即可.
对于②利用两集合间的包含关系转化为充分、必要性的关系;
对于③利用双曲线的标准方程满足的条件判断,即在此题方程形式下,只需前后两个分母异号即可;
对于④先算出焦点弦的长,和2比较即可.
解答:
解:①当定点落在定直线上时,该轨迹是一条过该点且与定直线垂直的射线,故①为假;
②因为N?M,a∈M不一定推出a∈N,所以前者是后者的不充分条件,故②为假;
③因为2sinθ∈[-2,2],所以3+2sinθ>0,易知sinθ-2<0,所以(2sinθ+3)(sinθ-2)<0,故该方程表示双曲线,故③为真;
④由题意得焦点为(±
,0),将x=
代入方程得y=±1,所以通径长为2,故直线l垂直于实轴,因此满足题意的直线只有1条,故④为真.
故答案为③④
②因为N?M,a∈M不一定推出a∈N,所以前者是后者的不充分条件,故②为假;
③因为2sinθ∈[-2,2],所以3+2sinθ>0,易知sinθ-2<0,所以(2sinθ+3)(sinθ-2)<0,故该方程表示双曲线,故③为真;
④由题意得焦点为(±
| 6 |
| 6 |
故答案为③④
点评:有关命题的考查一般以考查概念为主,题目可难可易,因此在做题时一定要在准确、深刻理解概念的基础上作答.

练习册系列答案
相关题目
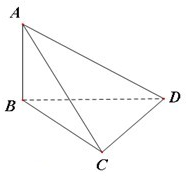 如图,AB⊥平面BCD,BD⊥CD,若AB=BC=2BD,则二面角B-AC-D的正弦值为
如图,AB⊥平面BCD,BD⊥CD,若AB=BC=2BD,则二面角B-AC-D的正弦值为