题目内容
若f（n）为n2+1（n∈N*）的各位数字之和，如：142+1=197，1+9+7=17，则f（14）=17；记f1（n）=f（n），f2（n）=f（f1（n）），f3（n）=f （f2（n）），…fk+1（n）=f（fk（n）），k∈N*，
则f2015（9）= ．
则f2015（9）=
考点：数列与函数的综合
专题：等差数列与等比数列
分析：利用已知条件求出数列的前几项，推出数列的特征周期数列，然后求解即可．
解答：
解：∵92+1=82，∴f1 （9）=f （9）=10；
∵102+1=101，∴f2 （9）=f （f1（9））=f （10）=2；
∵22+1=5，∴f3 （9）=f （f2（9））=f （2）=5；
∵52+1=26，∴f4 （9）=f （f3（9））=f （5）=8；
∵82+1=65，∴f5 （9）=f （f4（9））=f （8）=11；
∵112+1=122，∴f6 （9）=f （f5（9））=f （11）=5．
∴数列{ fn （9）}从第3项开始是以3为周期的循环数列
∵2015=2+671×3，
∴f 2015（9）=f 5（9）=11．
故答案为：11．
∵102+1=101，∴f2 （9）=f （f1（9））=f （10）=2；
∵22+1=5，∴f3 （9）=f （f2（9））=f （2）=5；
∵52+1=26，∴f4 （9）=f （f3（9））=f （5）=8；
∵82+1=65，∴f5 （9）=f （f4（9））=f （8）=11；
∵112+1=122，∴f6 （9）=f （f5（9））=f （11）=5．
∴数列{ fn （9）}从第3项开始是以3为周期的循环数列
∵2015=2+671×3，
∴f 2015（9）=f 5（9）=11．
故答案为：11．
点评：考查考查数列与函数相结合．考查阅读和推理能力．
练习册系列答案
阅读快车系列答案
相关题目
某几何体的三视图如图所示，则该几何体的体积为（ ）
| A、π | ||
| B、2π | ||
C、
| ||
D、
|
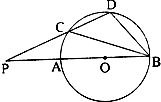如图，从圆O外一点P作圆O的割线 PAB、PCD． AB是圆O的直径，若PA=4，PC=5，CD=3，则∠CBD=数列{an}中，an+2=an+1-an，a1=2，a2=5，则a2015的值是（ ）
| A、-2 | B、2 | C、-5 | D、5 |
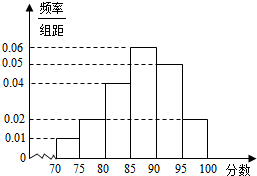某校为规范学生的行为，制定出一套科学有效的“德语百分制量化考核制度”，一领导小组将该校高三年级1200个学生随机编号为1、2、…、1200，现将编号能被30整除的40名学生抽取出来进行座谈，并将他们的考核分分成六段：[70，75），[75，80），[80，85），[85，90），[90，95），[95，100]，统计后得到如图的频率分布直方图：