题目内容
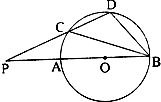 如图,从圆O外一点P作圆O的割线 PAB、PCD. AB是圆O的直径,若PA=4,PC=5,CD=3,则∠CBD=
如图,从圆O外一点P作圆O的割线 PAB、PCD. AB是圆O的直径,若PA=4,PC=5,CD=3,则∠CBD=考点:与圆有关的比例线段
专题:选作题,立体几何
分析:由于题目中并没有给出与角相关的已知条件,故解题的关键是构造三角形,解三角形求角的大小,故根据已知条件,结合割线定理,求出圆的半径是本题的切入点.
解答:
解:由割线长定理得:PA•PB=PC•PD,
即4×PB=5×(5+3),
∴PB=10,
∴AB=6,
∴R=3,
所以△OCD为正三角形,∠CBD=
∠COD=30°.
故答案为:30°.
即4×PB=5×(5+3),
∴PB=10,
∴AB=6,
∴R=3,
所以△OCD为正三角形,∠CBD=
| 1 |
| 2 |
故答案为:30°.
点评:当已知中的条件可以得到一个等边三角形、平行四边形、直角三角形等特殊图形,我们经常利用这些图形特有的性质,得到相关的数量关系,进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知数列{an}满足:
•
•
…
=
(n∈N*),则a10=( )
| lna1 |
| 2 |
| lna2 |
| 5 |
| lna3 |
| 8 |
| lnan |
| 3n-1 |
| 3n+2 |
| 2 |
| A、e26 |
| B、e29 |
| C、e32 |
| D、e35 |
已知集合 A={x|0<x<1},B={x|x≥1},则正确的是( )
| A、A∩B={x|0<x<1} |
| B、A∩B=∅ |
| C、A∪B={x|0<x<1} |
| D、A∪B=∅ |
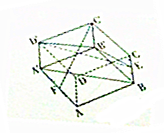 如图,在棱长为2的正方体AC′中,E,F为BC和AA′的中点
如图,在棱长为2的正方体AC′中,E,F为BC和AA′的中点