题目内容
已知数列{an}和{bn}满足,a1=1,a2=2,an>0,bn=
(n∈N+),且{bn}是以q为公比的等比数列
(1)求,an+2=anq2
(2)设cn=a2n-1+2a2n,试判断数列{cn}是否为等比数列,说明理由
(3)求和,S2n=
+
+
+
+…+
+
.
| anan+1 |
(1)求,an+2=anq2
(2)设cn=a2n-1+2a2n,试判断数列{cn}是否为等比数列,说明理由
(3)求和,S2n=
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a2n-1 |
| 1 |
| a2n |
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(1)直接由{bn}是以q为公比的等比数列结合bn=
加以证明;
(2)由an+2=anq2分别写出a2n-1、2a2n,得到cn=a2n-1+2a2n后即可判断数列{cn}是等比数列;
(3)由(2)求得
=
q2-2n,
=
q2-2n,代入S2n=
+
+
+
+…+
+
后分组,然后利用等比数列的前n项和得答案.
| anan+1 |
(2)由an+2=anq2分别写出a2n-1、2a2n,得到cn=a2n-1+2a2n后即可判断数列{cn}是等比数列;
(3)由(2)求得
| 1 |
| a2n-1 |
| 1 |
| a1 |
| 1 |
| a2n |
| 1 |
| a2 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a2n-1 |
| 1 |
| a2n |
解答:
(1)证明:由
=q,有
=
=q,∴an+2=anq2(n∈N+);
(2)解:{cn}是首项为5,以q2为公比的等比数列.
证明:∵an=qn-2q2,
∴a2n-1=a2n-3q2=…=a1q2n-2,
a2n=a2n-2q2=…=a2qn-2,
∴cn=a2n-1+2a2n=a1q2n-2+2a2q2n-2=(a1+2a2)q2n-2=5q2n-2.
∴{cn}是首项为5,以q2为公比的等比数列;
(3)解:由(2)得
=
q2-2n,
=
q2-2n,
于是S2n=
+
+
+
+…+
+
=(
+
+…+
)+(
+
+…+
)
=
(1+
+…+
)+
(1+
+…+
)
=
(1+
+…+
).
当q=1时,S2n=
+
+
+
+…+
+
=
(1+
+…+
)=
n;
当q≠1时,S2n=
+
+
+
+…+
+
=
(1+
+…+
)=
(
)=
[
].
| bn+1 |
| bn |
| ||
|
|
(2)解:{cn}是首项为5,以q2为公比的等比数列.
证明:∵an=qn-2q2,
∴a2n-1=a2n-3q2=…=a1q2n-2,
a2n=a2n-2q2=…=a2qn-2,
∴cn=a2n-1+2a2n=a1q2n-2+2a2q2n-2=(a1+2a2)q2n-2=5q2n-2.
∴{cn}是首项为5,以q2为公比的等比数列;
(3)解:由(2)得
| 1 |
| a2n-1 |
| 1 |
| a1 |
| 1 |
| a2n |
| 1 |
| a2 |
于是S2n=
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a2n-1 |
| 1 |
| a2n |
=(
| 1 |
| a1 |
| 1 |
| a3 |
| 1 |
| a2n-1 |
| 1 |
| a2 |
| 1 |
| a4 |
| 1 |
| a2n |
=
| 1 |
| a1 |
| 1 |
| q2 |
| 1 |
| q2n-2 |
| 1 |
| a2 |
| 1 |
| q2 |
| 1 |
| q2n-2 |
=
| 3 |
| 2 |
| 1 |
| q2 |
| 1 |
| q2n-2 |
当q=1时,S2n=
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a2n-1 |
| 1 |
| a2n |
| 3 |
| 2 |
| 1 |
| q2 |
| 1 |
| q2n-2 |
| 3 |
| 2 |
当q≠1时,S2n=
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a2n-1 |
| 1 |
| a2n |
| 3 |
| 2 |
| 1 |
| q2 |
| 1 |
| q2n-2 |
| 3 |
| 2 |
| 1-q-2n |
| 1-q-2 |
| 3 |
| 2 |
| q2n-1 |
| q2n-2(q2-1) |
点评:本题考查了数列递推式,考查了等比关系的确定,训练了数列的分组求和,考查了等比数列的前n项和,是中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
已知函数f(x)=lnx+
x2-2x+2在[et,+∞)(t∈Z)上有零点,则t的最大值为( )
| 3 |
| 8 |
| A、0 | B、-1 | C、-2 | D、2 |
已知集合 A={x|0<x<1},B={x|x≥1},则正确的是( )
| A、A∩B={x|0<x<1} |
| B、A∩B=∅ |
| C、A∪B={x|0<x<1} |
| D、A∪B=∅ |
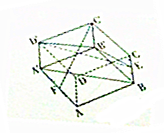 如图,在棱长为2的正方体AC′中,E,F为BC和AA′的中点
如图,在棱长为2的正方体AC′中,E,F为BC和AA′的中点