题目内容
对于关于x的不等式ax2-3x+6＞4，-------（*）
（1）若（*）对于任意实数x总成立，求实数a的取值范围；
（2）若（*）的解集为{x|x＜1或x＞b}，求不等式ax2-（ac+b）x+bc＜0的解集．
（1）若（*）对于任意实数x总成立，求实数a的取值范围；
（2）若（*）的解集为{x|x＜1或x＞b}，求不等式ax2-（ac+b）x+bc＜0的解集．
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：（1）对a分类讨论，利用“三个二次的关系”即可得出；
（2）由题意可得1，b为方程ax2-3x+2=0的根，解得a=1，b=2．不等式ax2-（ac+b）x+bc＜0化为x2-（2+c）x+2c＜0，即（x-2）（x-c）＜0．对c分类讨论即可得出．
（2）由题意可得1，b为方程ax2-3x+2=0的根，解得a=1，b=2．不等式ax2-（ac+b）x+bc＜0化为x2-（2+c）x+2c＜0，即（x-2）（x-c）＜0．对c分类讨论即可得出．
解答：
解：（1）当a=0时，由ax2-3x+6＞4得x＜
，不合题意；
当a≠0时，由题意知ax2-3x+2＞0对于任意实数x总成立，
则
，
解得a＞
，故实数a的取值范围是a＞
．
（2）∵1，b为方程ax2-3x+2=0的根，
解得a=1，b=2．
∵x2-（2+c）x+2c＜0，
∴（x-2）（x-c）＜0．
当c=2时，x∈∅．
当c＞2时，2＜x＜c．
当c＜2时，c＜x＜2．
| 2 |
| 3 |
当a≠0时，由题意知ax2-3x+2＞0对于任意实数x总成立，
则
|
解得a＞
| 9 |
| 8 |
| 9 |
| 8 |
（2）∵1，b为方程ax2-3x+2=0的根，
解得a=1，b=2．
∵x2-（2+c）x+2c＜0，
∴（x-2）（x-c）＜0．
当c=2时，x∈∅．
当c＞2时，2＜x＜c．
当c＜2时，c＜x＜2．
点评：本题考查了“三个二次的关系”、一元二次不等式的解法，考查了分类讨论的思想方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
已知不等式xy≤ax2+2y2对于x∈[1，2]，y∈[2，3]恒成立，则实数a的取值范围是（ ）
| A、[-1，+∞） |
| B、（-∞，1] |
| C、（0，2] |
| D、[-1，2] |
一个电路板上装有甲、乙两根保险丝，甲保险丝熔断的概率为0.085，乙保险丝熔断的概率为0.074，两根同时熔断的概率为0.063，则至少有一根熔断的概率为（ ）
| A、0.159 |
| B、0.085 |
| C、0.096 |
| D、0.074 |
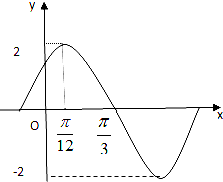已知函数f（x）=Acos（ωx+φ），（A＞0，ω＞0，|φ|＜