题目内容
5. 如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )
如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )| A. | 与m,n都有关 | B. | 与m,n都无关 | C. | 与m有关,与n无关 | D. | 与n有关,与m无关 |
分析 求出△EFG的面积和P到平面EFG的距离,代入棱锥的体积公式计算.
解答 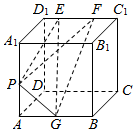 解:连结AD1,A1D,则AD1=2$\sqrt{2}$,A1D⊥平面ABC1D1,∴AA1与平面ABC1D1所成的角为∠A1AD1=45°,
解:连结AD1,A1D,则AD1=2$\sqrt{2}$,A1D⊥平面ABC1D1,∴AA1与平面ABC1D1所成的角为∠A1AD1=45°,
∴P到平面ABC1D1的距离d=AP•sin45°=$\frac{\sqrt{2}n}{2}$.
∵S△EFG=$\frac{1}{2}×EF×A{D}_{1}$=$\sqrt{2}$.
∴三棱锥P-EFG的体积V=$\frac{1}{3}•{S}_{△EFG}•d$=$\frac{n}{3}$.
故选:D.
点评 本题考查了正方体的结构特征,棱锥的体积计算,属于中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
17.某中学调查了某班全部50名同学参加数学兴趣小组和语文兴趣小组的情况,数据如表:(单位:人)
(1)从该班同学中随机选1名,求该同学至少参加上述一个兴趣小组的概率;
(2)在既参加数学兴趣小组,又参加语文兴趣小组的6个同学中,有4个男同学,2个女同学,现从这6个同学中随机抽取2人做进一步的调查,求抽取的2人中恰有1个女同学的概率.
| 参加数学兴趣小组 | 未参加数学兴趣小组 | |
| 参加语文兴趣小组 | 6 | 10 |
| 未参加语文兴趣小组 | 14 | 20 |
(2)在既参加数学兴趣小组,又参加语文兴趣小组的6个同学中,有4个男同学,2个女同学,现从这6个同学中随机抽取2人做进一步的调查,求抽取的2人中恰有1个女同学的概率.
15.若复数z满足iz=2-4i,则$\overline{z}$在复平面内对应的点的坐标是( )
| A. | (2,4) | B. | (2,-4) | C. | (-4,-2) | D. | (-4,2) |
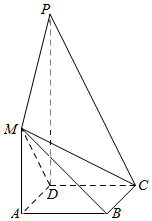 如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.
如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.