题目内容
13．已知复数z=a+bi（a，b∈R，b≠0，i为虚数单位），且2z+$\frac{1}{z}$为实数，求2z+$\frac{1}{z}$的取值范围．分析 利用复数的运算法则、复数为实数的充要条件即可得出．
解答 解：2z+$\frac{1}{z}$=2（a+bi）+$\frac{1}{a+bi}$=2a+2bi+$\frac{a-bi}{（a+bi）（a-bi）}$=2a+$\frac{a}{{a}^{2}+{b}^{2}}$+（2b-$\frac{b}{{a}^{2}+{b}^{2}}$）i为实数，
∴2b-$\frac{b}{{a}^{2}+{b}^{2}}$=0，b≠0，解得a2+b2=$\frac{1}{2}$．
∵b≠0，∴a∈$（-\frac{\sqrt{2}}{2}，\frac{\sqrt{2}}{2}）$．
∴2z+$\frac{1}{z}$=2a+2a=4a∈$（-2\sqrt{2}，2\sqrt{2}）$．
点评 本题考查了数的运算法则、复数为实数的充要条件，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
5．
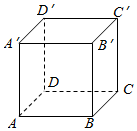如图，正方体ABCD-A′B′C′D′的棱长为2，动点E，F在棱D′C′上．点G是AB的中点，动点P在棱A′A上，若EF=1，D′E=m，AP=n，则三棱锥P-EFG的体积（ ）
如图，正方体ABCD-A′B′C′D′的棱长为2，动点E，F在棱D′C′上．点G是AB的中点，动点P在棱A′A上，若EF=1，D′E=m，AP=n，则三棱锥P-EFG的体积（ ）| A． | 与m，n都有关 | B． | 与m，n都无关 | C． | 与m有关，与n无关 | D． | 与n有关，与m无关 |
2．甲、乙两人玩数字游戏，先由甲在一张卡片上任意写出一个数字，记为a，再由乙猜甲刚才写出的数字，把乙猜出的数字记为b，且a，b∈{1，2，3}，若|a-b|≤1，则乙获胜，现甲、乙两人玩一次这个游戏，则乙获胜的概率为（ ）
| A． | $\frac{7}{9}$ | B． | $\frac{2}{3}$ | C． | $\frac{5}{9}$ | D． | $\frac{1}{3}$ |