题目内容
16.若函数f(x)=xln(x+$\sqrt{2a+{x}^{2}}$)的图象关于y轴对称,则a=$\frac{1}{2}$.分析 利用函数图象的对称性得出f(-x)=f(x),代入求解即可.
解答 解:f(x)=xln(x+$\sqrt{2a+{x}^{2}}$)的图象关于y轴对称,
∴f(-x)=f(x)
即-xln(-x+$\sqrt{2a+{x}^{2}}$)=xln(x+$\sqrt{2a+{x}^{2}}$),
∴$\frac{1}{-x+\sqrt{2a+{x}^{2}}}$=x+$\sqrt{2a+{x}^{2}}$,
解得a=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题简单的考查了函数的性质,与函数图象,关键是判断出是偶函数即可.

练习册系列答案
相关题目
7.在等比数列{an}中,已知a2+a3=1,a3+a4=$\sqrt{2}$,则a14+a15等于( )
| A. | 16 | B. | 32 | C. | 64 | D. | 128 |
5.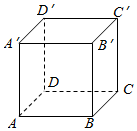 如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )
如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )
 如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )
如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )| A. | 与m,n都有关 | B. | 与m,n都无关 | C. | 与m有关,与n无关 | D. | 与n有关,与m无关 |