题目内容
20.等差数列{an}共有2n-1项,其中奇数项之和为144,偶数项之和为132,则an为12.分析 设等差数列{an}的公差为d,由题意可得:a1+a3+…+a2n-1=144,a2+a4+…+a2n-2=132,两式相减即可得出.
解答 解:设等差数列{an}的公差为d,
由题意可得:a1+a3+…+a2n-1=144,
a2+a4+…+a2n-2=132,
则a1+(n-1)d=12,
∴an=12.
故答案为:12.
点评 本题考查了等差数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
5.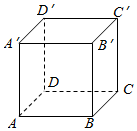 如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )
如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )
 如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )
如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )| A. | 与m,n都有关 | B. | 与m,n都无关 | C. | 与m有关,与n无关 | D. | 与n有关,与m无关 |
9.某超市某种面包进货价为每个4元,实际售价为每个4.5元,若当天不能卖完,就在闭店前以每个3元的价格全部处理,据以往统计日需求量(单位:个)的情况如表:
若某日超市面包进货量为600.
(1)若以日需求量x所在区间的中间值为估计值,根据上表列出当日利润y的分布列;
(2)估计超市当日利润y的均值.
| 日需求量x | (0,400] | (400,600] | (600,800] | (800,1000] |
| 频率 | 0.2 | 0.4 | 0.3 | 0.1 |
(1)若以日需求量x所在区间的中间值为估计值,根据上表列出当日利润y的分布列;
(2)估计超市当日利润y的均值.
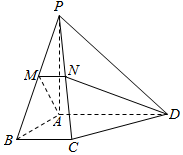 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.