题目内容
15．若复数z满足iz=2-4i，则$\overline{z}$在复平面内对应的点的坐标是（ ）| A． | （2，4） | B． | （2，-4） | C． | （-4，-2） | D． | （-4，2） |
分析 把已知等式变形，利用复数代数形式的乘除运算化简求得z，进一步求得$\overline{z}$得答案．
解答 解：由iz=2-4i，得
$z=\frac{2-4i}{i}=\frac{（2-4i）（-i）}{-{i}^{2}}=-4-2i$，
∴$\overline{z}=-4+2i$，
∴$\overline{z}$在复平面内对应的点的坐标是（-4，2），
故选：D．
点评 本题考查复数代数形式的乘除运算，考查了共轭复数的概念，是基础题．
练习册系列答案
相关题目
5．
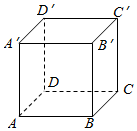如图，正方体ABCD-A′B′C′D′的棱长为2，动点E，F在棱D′C′上．点G是AB的中点，动点P在棱A′A上，若EF=1，D′E=m，AP=n，则三棱锥P-EFG的体积（ ）
如图，正方体ABCD-A′B′C′D′的棱长为2，动点E，F在棱D′C′上．点G是AB的中点，动点P在棱A′A上，若EF=1，D′E=m，AP=n，则三棱锥P-EFG的体积（ ）| A． | 与m，n都有关 | B． | 与m，n都无关 | C． | 与m有关，与n无关 | D． | 与n有关，与m无关 |
20．《九章算术》是我国古代的数学名著，书中有如下问题：“今有五人分五钱，令上二人所得与下三人等．问各得几何．”其意思为“已知甲、乙、丙、丁、戊五人分5钱，甲、乙两人所得与丙、丁、戊三人所得相同，且甲、乙、丙、丁、戊所得依次成等差数列．问五人各得多少钱？”（“钱”是古代的一种重量单位）．这个问题中，甲所得为（ ）
| A． | $\frac{5}{4}$钱 | B． | $\frac{4}{3}$钱 | C． | $\frac{3}{2}$钱 | D． | $\frac{5}{3}$钱 |
7．将函数y=sin2x的图象向左平移$\frac{π}{4}$个单位得到函数f（x）的图象，则f（x）=（ ）
| A． | cos2x | B． | sin（2x+$\frac{π}{4}$） | C． | -cos2x | D． | -sin2x |
4．已知a，b∈R，则“a＞0，b＞0”是“a2+b2≥2ab”的（ ）
| A． | 既不充分也不要条件 | B． | 充分不必要条件 | ||
| C． | 必要不充分条件 | D． | 充分必要条件 |