题目内容
15.已知函数f(x)=$\sqrt{2}$cos(ωx-$\frac{π}{12}$)(其中ω>0,x∈R),图象上相邻两个最高点的距离为2π.(1)求f(-$\frac{π}{6}$)的值;
(2)若cosθ=$\frac{3}{5}$,θ∈($\frac{3π}{2}$,2π),求f(θ+$\frac{7π}{12}$).
分析 (1)根据周期求出f(x)解析式,代入数值计算;
(2)根据θ的范围求出sinθ,使用诱导公式求出答案.
解答 解:(1)∵f(x)图象上相邻两个最高点的距离为2π,
∴f(x)的周期T=$\frac{2π}{ω}=2π$,∴ω=1.
∴f(x)=$\sqrt{2}cos$(x-$\frac{π}{12}$).
∴f(-$\frac{π}{6}$)=$\sqrt{2}$cos(-$\frac{π}{4}$)=1.
(2)∵θ∈($\frac{3π}{2}$,2π),∴sinθ=-$\sqrt{1-co{s}^{2}θ}$=-$\frac{4}{5}$.
∴f($θ+\frac{7π}{12}$)=$\sqrt{2}$cos(θ$+\frac{π}{2}$)=-$\sqrt{2}$sinθ=$\frac{4\sqrt{2}}{5}$.
点评 本题考查了余弦函数的图象与性质,同角三角函数的关系,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
7.在等比数列{an}中,已知a2+a3=1,a3+a4=$\sqrt{2}$,则a14+a15等于( )
| A. | 16 | B. | 32 | C. | 64 | D. | 128 |
5.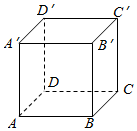 如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )
如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )
 如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )
如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )| A. | 与m,n都有关 | B. | 与m,n都无关 | C. | 与m有关,与n无关 | D. | 与n有关,与m无关 |