题目内容
10.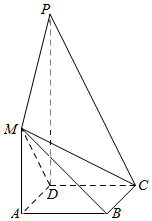 如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.
如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.(Ⅰ)求证:MB∥平面PDC;
(Ⅱ)求证:PM⊥平面MDC;
(Ⅲ)求三棱锥P-MDC的体积.
分析 (I)由AB∥CD,MA∥PD可得平面MAB∥平面PDC,故MB∥平面PDC;
(II)由平面ABCD⊥平面AMPD可得CD⊥平面AMPD,故CD⊥PM,由勾股定理计算MP,MD,可得MP2+MD2=PD2,即PM⊥MD,于是MP⊥平面MDC;
(III)以△MDC为棱锥的底面,则PM为棱锥的高,代入体积公式计算即可.
解答 解:(Ⅰ)∵四边形ABCD是正方形,
∴AB∥CD,
又∵MA∥PD,AB∩MA=A,CD∩PD=D,AB?平面ABM,MA?平面ABMCD?平面PDC,PD?平面PDC,
∴平面ABM∥平面PDC,
∵MB?平面ABM,
∴MB∥平面PDC.
(Ⅱ)∵平面ABCD⊥平面AMPD,平面ABCD∩平面AMPD=AD,CD⊥AD,CD?平面ABCD,
∴CD⊥平面AMPD,∵PM?平面AMPD,
∴CD⊥PM.
∵在直角梯形AMPD中,由$MA=AD=\frac{1}{2}PD=1$,得$MD=PM=\sqrt{2}$,
∴PM2+MD2=PD2,∴MD⊥PM,
又CD∩MD=D,CD?平面MDC,MD?平面MDC,
∴PM⊥平面MDC.
(Ⅲ)由(Ⅱ)知PM是三棱锥P-MDC的高,${S_{△MDC}}=\frac{1}{2}CD•MD=\frac{{\sqrt{2}}}{2}$.
∴三棱锥P-MDC的体积$V=\frac{1}{3}{S_{△MDC}}•PM=\frac{1}{3}$.
点评 本题考查了线面平行,线面垂直的判定,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
5.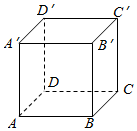 如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )
如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )
 如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )
如图,正方体ABCD-A′B′C′D′的棱长为2,动点E,F在棱D′C′上.点G是AB的中点,动点P在棱A′A上,若EF=1,D′E=m,AP=n,则三棱锥P-EFG的体积( )| A. | 与m,n都有关 | B. | 与m,n都无关 | C. | 与m有关,与n无关 | D. | 与n有关,与m无关 |
15.将y=sin2x+cos2x的图象向右平移$\frac{π}{4}$个单位后,所得图象的解析式是( )
| A. | y=sin2x-cos2x | B. | y=cos2x-sin2x | C. | y=cos2x+sin2x | D. | y=cosxsinx |
2.甲、乙两人玩数字游戏,先由甲在一张卡片上任意写出一个数字,记为a,再由乙猜甲刚才写出的数字,把乙猜出的数字记为b,且a,b∈{1,2,3},若|a-b|≤1,则乙获胜,现甲、乙两人玩一次这个游戏,则乙获胜的概率为( )
| A. | $\frac{7}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{9}$ | D. | $\frac{1}{3}$ |
20.《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,甲所得为( )
| A. | $\frac{5}{4}$钱 | B. | $\frac{4}{3}$钱 | C. | $\frac{3}{2}$钱 | D. | $\frac{5}{3}$钱 |