题目内容
20.设函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+2(x≤0)}\\{{e}^{x}-1(x>0)}\end{array}\right.$,若函数y=f(x)-2x+b有两个零点,则参数b的取值范围是(-∞,-2]∪(0,2ln2-1).分析 由y=f(x)-2x+b=0得f(x)=2x-b,作出函数f(x)和y=2x-b的图象,利用数形结合进行求解即可.
解答  解:作出函数f(x)的图象如图:,
解:作出函数f(x)的图象如图:,
由y=f(x)-2x+b=0得f(x)=2x-b,
当g(x)=2x-b经过点(0,2)时,满足两个函数有两个交点,
此时-b=2,即b=-2,当-b≥2,即b≤-2时,满足条件,
当g(x)=2x-b与f(x)=ex-1相切时,
由f′(x)=ex=2得x=ln2,y=eln2-1=2-1=1,即切点坐标为(ln2,1),
此时2ln2-b=1,即b=2ln2-1,
当直线g(x)=2x-b经过原点时,b=0,
∴要使两个函数有两个交点,
则此时0<b<2ln2-1,
综上0<b<2ln2-1或b≤-2,
故实数b的取值范围是(-∞,-2]∪(0,2ln2-1),
故答案为:(-∞,-2]∪(0,2ln2-1)
点评 本题主要考查函数零点个数的判断,根据函数与方程之间的关系转化为两个函数的交点个数问题是解决本题的关键.注意要利用数形结合.

练习册系列答案
相关题目
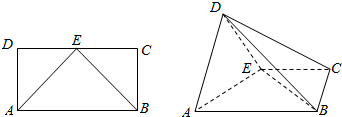 如图,在长方形ABCD中,AB=2,AD=1,E为CD的中点,以AE为折痕,把△DAE折起为△D′AE,且平面D′AE⊥平面ABCE.
如图,在长方形ABCD中,AB=2,AD=1,E为CD的中点,以AE为折痕,把△DAE折起为△D′AE,且平面D′AE⊥平面ABCE.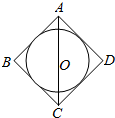 如图,圆O内切于正方形ABCD,将圆O、正方形ABCD绕直线AC旋转一周得到的两个旋转体的体积依次记为V1V2,则V1:V2=$\sqrt{2}:1$.
如图,圆O内切于正方形ABCD,将圆O、正方形ABCD绕直线AC旋转一周得到的两个旋转体的体积依次记为V1V2,则V1:V2=$\sqrt{2}:1$.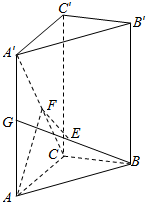 已知直三棱柱ABC-A′B′C′中,∠ACB=90°,BE=GE,AG=A′G,F是线段A′C上的点,EF∥平面ACB.
已知直三棱柱ABC-A′B′C′中,∠ACB=90°,BE=GE,AG=A′G,F是线段A′C上的点,EF∥平面ACB.