题目内容
10.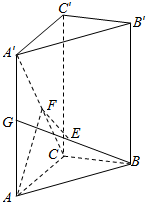 已知直三棱柱ABC-A′B′C′中,∠ACB=90°,BE=GE,AG=A′G,F是线段A′C上的点,EF∥平面ACB.
已知直三棱柱ABC-A′B′C′中,∠ACB=90°,BE=GE,AG=A′G,F是线段A′C上的点,EF∥平面ACB.(I)求证:BC⊥AF;
(2)若$\frac{CF}{CA′}$=λ,求λ的值.
分析 (1)由已知得AA′⊥BC,AC⊥BC,从而BC⊥平面ACC′A′,由此能证明BC⊥AF.
(2)以C为原点,CA为x轴,CB为y轴,CC′为z轴,建立空间直角坐标系,利用向量法能求出$λ=\frac{1}{4}$.
解答  证明:(1)∵直三棱柱ABC-A′B′C′中,∠ACB=90°,
证明:(1)∵直三棱柱ABC-A′B′C′中,∠ACB=90°,
∴AA′⊥BC,AC⊥BC,
∵AC∩BC=C,∴BC⊥平面ACC′A′,
∵F是线段A′C上的点,∴AF?平面ACC′A′,
∴BC⊥AF.
解:(2)以C为原点,CA为x轴,CB为y轴,CC′为z轴,建立空间直角坐标系,
∵BE=GE,AG=A′G,F是线段A′C上的点,EF∥平面ACB,
设AC=a,BC=b,AA1=c,
∴B(0,b,0),G(a,0,$\frac{c}{2}$),E($\frac{a}{2},\frac{b}{2},\frac{c}{4}$),A′(a,0,c),
∵$\frac{CF}{CA′}$=λ,∴F(λa,0,λc),∴$\overrightarrow{EF}$=($λa-\frac{a}{2}$,-$\frac{b}{2}$,$λc-\frac{c}{4}$),
∵平面ABC的法向量$\overrightarrow{n}$=(0,0,1),
∴$\overrightarrow{n}•\overrightarrow{EF}$=$λc-\frac{c}{4}$=0,解得$λ=\frac{1}{4}$.
点评 本题考查异面直线垂直的证明,考查满足条件的实数值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
2.P={x|2x2-7x+5<0},Q={x|0<x<10},那么( )
| A. | P∩Q=∅ | B. | P⊆Q | C. | Q⊆P | D. | P∪Q=R |
8.已知函数f(ex)=x,则f(2)=( )
| A. | 2 | B. | e2 | C. | log2e | D. | ln2 |
9.(重点中学做)设实数x,y满足$\left\{\begin{array}{l}{x-y-2≤0}\\{x+3y-6≥0}\\{y-2≤0}\end{array}\right.$,则 z=x2+y2的取值范围是( )
| A. | [2,2$\sqrt{5}$] | B. | [10,20] | C. | [4,20] | D. | [$\frac{18}{5}$,20] |