题目内容
12.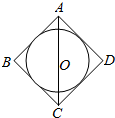 如图,圆O内切于正方形ABCD,将圆O、正方形ABCD绕直线AC旋转一周得到的两个旋转体的体积依次记为V1V2,则V1:V2=$\sqrt{2}:1$.
如图,圆O内切于正方形ABCD,将圆O、正方形ABCD绕直线AC旋转一周得到的两个旋转体的体积依次记为V1V2,则V1:V2=$\sqrt{2}:1$.
分析 根据球的体积公式和圆锥的体积公式,分别求出V1,V2,可得答案.
解答 解:设AC=BD=2,
则正方形ABCD旋转后得到两个底面半径为1,高为1的圆锥形成的组合体,
故V1=2×$\frac{1}{3}$×π=$\frac{2π}{3}$,
圆O绕对角线AC旋转一周得到一个半径为$\frac{\sqrt{2}}{2}$的球,
故V2=$\frac{4π}{3}$($\frac{\sqrt{2}}{2}$)3=$\frac{\sqrt{2}π}{3}$,
故V1:V2=$\frac{2π}{3}$:$\frac{\sqrt{2}π}{3}$=$\sqrt{2}:$1,
故答案为:$\sqrt{2}:1$.
点评 本题考查的知识点是旋转体,熟练掌握圆锥和球的体积公式,是解答的关键.

练习册系列答案
相关题目
2.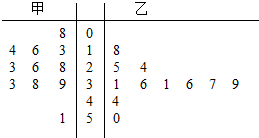 如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,其中茎为十位数,叶为个位数,甲、乙两人得分的中位数为X甲、X乙,则下列判断正确的是( )
如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,其中茎为十位数,叶为个位数,甲、乙两人得分的中位数为X甲、X乙,则下列判断正确的是( )
 如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,其中茎为十位数,叶为个位数,甲、乙两人得分的中位数为X甲、X乙,则下列判断正确的是( )
如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,其中茎为十位数,叶为个位数,甲、乙两人得分的中位数为X甲、X乙,则下列判断正确的是( )| A. | X乙-X甲=5,甲比乙得分稳定 | B. | X乙-X甲=5,乙比甲得分稳定 | ||
| C. | X乙-X甲=10,甲比乙得分稳定 | D. | X乙-X甲=10,乙比甲得分稳定 |
7.已知某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
2.P={x|2x2-7x+5<0},Q={x|0<x<10},那么( )
| A. | P∩Q=∅ | B. | P⊆Q | C. | Q⊆P | D. | P∪Q=R |
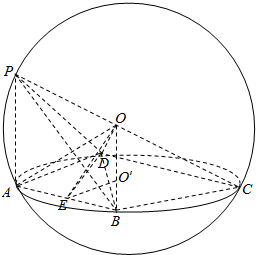 已知点P,A,B,C,D是球O表面上的点,且球心O在线段PC上,PA⊥平面ABCD,E为AB的中点,∠BCD=90°
已知点P,A,B,C,D是球O表面上的点,且球心O在线段PC上,PA⊥平面ABCD,E为AB的中点,∠BCD=90° 如图,一个几何体的三视图是一个全等的等腰直角三角形,且直角边长为2,则这个几何体的外接球的表面积为12π.
如图,一个几何体的三视图是一个全等的等腰直角三角形,且直角边长为2,则这个几何体的外接球的表面积为12π.