题目内容
8.已知x∈(1,5),则函数y=$\frac{2}{x-1}$+$\frac{1}{5-x}$的最小值为$\frac{3+2\sqrt{2}}{4}$.分析 求函数的导数,利用导数研究函数的单调性,结合函数最值和导数之间的关系进行求解即可.
解答 解:函数的导数f′(x)=-$\frac{2}{(x-1)^{2}}$+$\frac{1}{(x-5)^{2}}$=$\frac{2(x-5)^{2}-(x-1)^{2}}{(x-1)^{2}(x-5)^{2}}$=$\frac{{x}^{2}-18x+49}{(x-1)^{2}(x-5)^{2}}$,
由f′(x)=0得x2-18x+49=0得x=$\frac{18±\sqrt{1{8}^{2}-4×49}}{2}$=$\frac{18±8\sqrt{2}}{2}$=9±4$\sqrt{2}$,
∵x∈(1,5),
∴x=9-4$\sqrt{2}$,
当1<x<9-4$\sqrt{2}$时,f′(x)<0,函数单调递减,
当9-4$\sqrt{2}$<x<5时,f′(x)>0,函数单调递增,
故当x=9-4$\sqrt{2}$时,函数f(x)取得极小值,同时也是最小值,此时f(9-4$\sqrt{2}$)=$\frac{2}{9-4\sqrt{2}-1}$+$\frac{1}{5-9+4\sqrt{2}}$
=$\frac{2}{8-4\sqrt{2}}$+$\frac{1}{4\sqrt{2}-4}$=$\frac{1}{4-2\sqrt{2}}$+$\frac{1}{4\sqrt{2}-4}$=$\frac{4+2\sqrt{2}}{16-8}$+$\frac{4\sqrt{2}+4}{32-16}$=$\frac{4+2\sqrt{2}}{8}$+$\frac{4\sqrt{2}+4}{16}$
=$\frac{2+\sqrt{2}}{4}$+$\frac{\sqrt{2}+1}{4}$=$\frac{3+2\sqrt{2}}{4}$,
故答案为:$\frac{3+2\sqrt{2}}{4}$
点评 本题主要考查函数最值的求解,求函数的导数,利用导数研究函数的单调性和最值是解决本题的关键.考查学生的运算和推理能力.

 阅读快车系列答案
阅读快车系列答案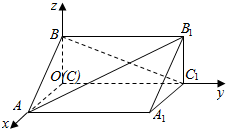 如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=2CB,CC1=3CB,则直线BC1与直线AB1夹角的余弦值为( )
如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=2CB,CC1=3CB,则直线BC1与直线AB1夹角的余弦值为( )| A. | $\frac{4\sqrt{35}}{35}$ | B. | $\frac{\sqrt{35}}{70}$ | C. | $\frac{2\sqrt{35}}{35}$ | D. | $\frac{2}{35}$ |
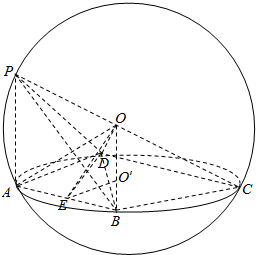 已知点P,A,B,C,D是球O表面上的点,且球心O在线段PC上,PA⊥平面ABCD,E为AB的中点,∠BCD=90°
已知点P,A,B,C,D是球O表面上的点,且球心O在线段PC上,PA⊥平面ABCD,E为AB的中点,∠BCD=90°