题目内容
10.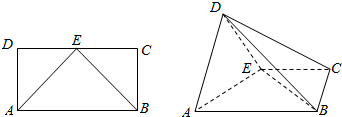 如图,在长方形ABCD中,AB=2,AD=1,E为CD的中点,以AE为折痕,把△DAE折起为△D′AE,且平面D′AE⊥平面ABCE.
如图,在长方形ABCD中,AB=2,AD=1,E为CD的中点,以AE为折痕,把△DAE折起为△D′AE,且平面D′AE⊥平面ABCE.(1)求证:AD′⊥BE;
(2)求三棱锥D′-ABE的体积;
(3)求D′E与BC所成角的大小.
分析 (1)取AE中点F,连结D′F,BF,计算D′B,由勾股定理的逆定理可推出AD′⊥DB,由折叠的性质可得AD′⊥D′E,故而AD′⊥平面BD′E,从而推出AD′⊥BE;
(2)V棱锥D′-ABE=$\frac{1}{3}$S△ABE•D′F=$\frac{1}{3}×\frac{1}{2}×AE×BE×D′F$;
(3)过E做EM∥BC,交AB于M,连结D′M,则,∠MED′为D′E与BC所成的角.计算△D′ME的三边长,得出∠MED′的大小.
解答  证明:(1)取AE中点F,连结D′F,BF,
证明:(1)取AE中点F,连结D′F,BF,
∵AD′=D′E=1,∠AD′E=90°,∴D′F⊥AE,D′F=EF=$\frac{1}{2}AE$=$\frac{\sqrt{2}}{2}$.
∵平面D′AE⊥平面ABCE,平面D′AE∩平面ABCE=AE,D′F?平面D′AE,D′F⊥AE,
∴D′F⊥平面ABCE,∵BF?平面ABCE,
∴D′F⊥BF,
∵∠AED′=∠BEC=45°,∴BE⊥AE,
∴BF=$\sqrt{B{E}^{2}+E{F}^{2}}$=$\frac{\sqrt{10}}{2}$,∴BD′=$\sqrt{D′{F}^{2}+B{F}^{2}}$=$\sqrt{3}$.
∵AD′=1,AB=2,∴AD′2+BD′2=AB2,∴AD′⊥BD′.
又∵AD′⊥D′E,D′E?平面BD′E,BD′?平面BD′E,D′E∩BD′=D′,
∴AD′⊥平面BD′E,∵BE?平面BD′E,
∴AD′⊥BE.
(2)V棱锥D′-ABE=$\frac{1}{3}$S△ABE•D′F=$\frac{1}{3}×\frac{1}{2}×AE×BE×D′F$=$\frac{1}{3}×\frac{1}{2}×\sqrt{2}×\sqrt{2}×\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{6}$.
(3)过E做EM∥BC,交AB于M,连结D′M,则M为AB的中点,∠MED′为D′E与BC所成的角.
∵AD′⊥BD′,∴D′M=$\frac{1}{2}AB$=1,∵D′E=1,ME=BC=1,
∴△D′ME是等边三角形,∴∠MED′=60°.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,异面直线所成的角,正确作出空间角是解题关键.

| A. | -3或2 | B. | 2 | C. | 3 | D. | -3 |
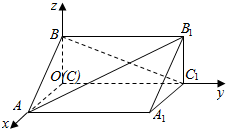 如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=2CB,CC1=3CB,则直线BC1与直线AB1夹角的余弦值为( )
如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=2CB,CC1=3CB,则直线BC1与直线AB1夹角的余弦值为( )| A. | $\frac{4\sqrt{35}}{35}$ | B. | $\frac{\sqrt{35}}{70}$ | C. | $\frac{2\sqrt{35}}{35}$ | D. | $\frac{2}{35}$ |
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
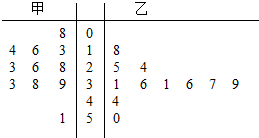 如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,其中茎为十位数,叶为个位数,甲、乙两人得分的中位数为X甲、X乙,则下列判断正确的是( )
如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,其中茎为十位数,叶为个位数,甲、乙两人得分的中位数为X甲、X乙,则下列判断正确的是( )| A. | X乙-X甲=5,甲比乙得分稳定 | B. | X乙-X甲=5,乙比甲得分稳定 | ||
| C. | X乙-X甲=10,甲比乙得分稳定 | D. | X乙-X甲=10,乙比甲得分稳定 |