题目内容
设全集U=R，集合A={x||x-1|≤1}，B={x|y=2x，y＞1}，则A∩（∁UB）=（ ）
| A、∅ |
| B、{0} |
| C、{x|0≤x≤2} |
| D、{x|x≤2} |
考点：交、并、补集的混合运算
专题：集合
分析：求出集合A，B，利用集合的基本运算即可得到结论
解答：
解：A={x||x-1|≤1}={x|0≤x≤2}，B={x|y=2x，y＞1}={x|x＞0}，
∴（∁UB）={x|x≤0}，
即A∩（∁UB）═{x|x=0}={0}，
故选：B
∴（∁UB）={x|x≤0}，
即A∩（∁UB）═{x|x=0}={0}，
故选：B
点评：本题主要考查集合的基本运算，利用条件求出集合A，B是解决本题的关键，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
已知a，b∈R，则“a+b＞0且ab＞0”是“a＞0且b＞0”成立的（ ）
| A、充分不必要 |
| B、必要不充分 |
| C、充要条件 |
| D、既不充分也不必要 |
（x2-
）6的展开式中，常数项等于（ ）
| 1 |
| x |
| A、15 | B、10 |
| C、-15 | D、-10 |
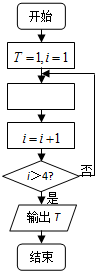
如图所示的程序框图，若执行运算1×
×
×
×
，则在空白执行框中，应该填入（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| A、T=T•（i+1） | ||
| B、T=T•i | ||
C、T=T•
| ||
D、T=T•
|
不等式|x|（1-x2）＞0的解集是（ ）
| A、（-1，1） |
| B、（-1，0）∪（0，1） |
| C、（-∞，-1）∪（1，+∞） |
| D、（-∞，-1）∪（0，1） |
下列有关命题的说法正确的是（ ）
A、“θ≠60°”是“cosθ≠
| ||
| B、“x=2”是“x2-5x+6=0”的必要不充分条件 | ||
| C、命题“?x∈R，使得x2+x+1＜0”的否定是：“?x∈R，均有x2+x+1＜0” | ||
| D、命题“若x=y，则sinx=siny”的逆否命题为真命题 |
已知f（x）是定义在R上的偶函数，函数周期为2，且在区间[0，1]上是增函数，则f（-5.5）、f（-1）、f（2）的大小关系是（ ）
| A、f（-5.5）＜f（2）＜f（-1） |
| B、f（-1）＜f（-5.5）＜f（2） |
| C、f（2）＜f（-5.5）＜f（-1） |
| D、f（-1）＜f（2）＜f（-5.5） |
如图，已知二次函数为y=x2，求抛物线与x=1和x轴组成的封闭图形的面积．