题目内容
定积分
dx-
sinxdx的值为 ．
| ∫ | e 1 |
| 1 |
| x |
| ∫ | 1 0 |
考点：定积分
专题：计算题,导数的综合应用
分析：先找到被积函数的原函数，然后运用微积分基本定理计算定积分即可．
解答：
解：
dx-
sinxdx
=lnx
+cosx
=lne-ln1+cos1-cos0
=1+cos1-1
=cos1．
故答案为：cos1．
| ∫ | e 1 |
| 1 |
| x |
| ∫ | 1 0 |
=lnx
| | | e 1 |
| | | 1 0 |
=lne-ln1+cos1-cos0
=1+cos1-1
=cos1．
故答案为：cos1．
点评：本题主要考查了定积分，运用微积分基本定理计算定积分的关键是找到被积函数的原函数，属于积分中的基础题．
练习册系列答案
相关题目
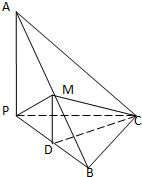如图，已知三棱锥A-PBC中，AC⊥BC，AP⊥PC，M为AB的中点，D为PB的中点，且△PMB为正三角形．
设全集U=R，集合A={x||x-1|≤1}，B={x|y=2x，y＞1}，则A∩（∁UB）=（ ）
| A、∅ |
| B、{0} |
| C、{x|0≤x≤2} |
| D、{x|x≤2} |