题目内容
设f（x）是R上的奇函数，且f（x+2）=-f（x），当0≤x≤1时，f（x）=x，则f（4.5）= ．
考点：抽象函数及其应用
专题：函数的性质及应用
分析：利用奇函数定义与条件f（x+2）=-f（x），把f（4.5）的自变量转化到[0，1]的范围内即可．
解答：
解：因为f（x+2）=-f（x），
所以f（4.5）=-f（2.5），f（2.5）=-f（0.5），
所以f（4.5）=f（0.5）．
因为0≤x≤1时，f（x）=x，
故f（4.5）=f（0.5）=0.5
故答案为：0.5．
所以f（4.5）=-f（2.5），f（2.5）=-f（0.5），
所以f（4.5）=f（0.5）．
因为0≤x≤1时，f（x）=x，
故f（4.5）=f（0.5）=0.5
故答案为：0.5．
点评：本题考查奇函数定义及f（x+T）=-f（x）的应用，基本知识的考查．
练习册系列答案
相关题目
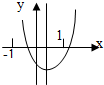已知二次函数f（x）=ax2+bx+c（a≠0）的图象如图所示，设M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b，则（ ）| A、M＞0 | B、M≥0 |
| C、M＜0 | D、M=0 |
