题目内容
9.定义在R上的函数f(x)=$\frac{g(x)}{{2}^{x}}$,g(x)=g(2-x)•4x-1,若f(x)在[1,+∞)为增函数,则( )| A. | g(1)>2g(0) | B. | g(3)>8g(0) | C. | g(2)>2g(0) | D. | g(4)<16g(0) |
分析 由已知函数f(x)=$\frac{g(x)}{{2}^{x}}$在[1,+∞)为增函数,可得f(3)>f(2),即g(3)>2g(2),进而根据g(x)=g(2-x)•4x-1,转化可得答案.
解答 解:∵函数f(x)=$\frac{g(x)}{{2}^{x}}$在[1,+∞)为增函数,
∴f(3)>f(2),即$\frac{g(3)}{{2}^{3}}$>$\frac{g(2)}{{2}^{2}}$,
即g(3)>2g(2),
又∵g(x)=g(2-x)•4x-1,
∴g(2)=g(2-2)•4=4g(0),
故g(3)>8g(0),
故选:B
点评 本题考查的知识点是函数单调性的性质,转化思想,难度中档.

练习册系列答案
相关题目
19.已知α是第二象限角,则由sinα=$\frac{\sqrt{3}}{2}$可推出cosα=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
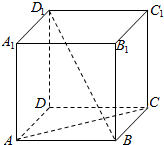 已知正方体ABCD-A1B1C1D1的棱长是a,用向量法证明AC⊥BD1.
已知正方体ABCD-A1B1C1D1的棱长是a,用向量法证明AC⊥BD1.