题目内容
19.已知函数f(x)=|x+a|-|x+2|-2a.(1)当a=-1时,求不等式f(x)≤0的解集;
(2)若不等式f(x)≤0恒成立,求实数a的取值范围.
分析 (1)当a=-1时,函数f(x)=|x-1|-|x+2|+2,利用零点分段法,分别求出各段上满足f(x)≤0的x的范围,综合讨论结果,可得答案;
(2)若不等式f(x)≤0恒成立,则|x+a|-|x+2|≤2a.即|a-2|≤2a恒成立,解得答案.
解答 解:(1)当a=-1时,函数f(x)=|x-1|-|x+2|+2,
当x≤-2时,不等式f(x)≤0可化为:5≤0,恒不成立;
当-2<x<1时,不等式f(x)≤0可化为:-2x+1≤0,解得:x≥$\frac{1}{2}$,
故$\frac{1}{2}$≤x<1;
当x≥1时,不等式f(x)≤0可化为:-1≤0,恒成立;
综上可得不等式f(x)≤0的解集为:[$\frac{1}{2}$,+∞);
(2)若不等式f(x)≤0恒成立,
则|x+a|-|x+2|≤2a.
即|a-2|≤2a恒成立,
即-2a≤a-2≤2a恒成立,
解得:a≥$\frac{2}{3}$
点评 本题考查的知识是分段函数的应用,恒成立问题,分类讨论思想,难度中档.

练习册系列答案
相关题目
14.若实数x,y满足$\left\{\begin{array}{l}{y≥2x-2}\\{y≥-x+1}\\{y≤x+1}\end{array}\right.$,则z=2x-y的最小值为( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
4.如图,平行四边形ABCD中,AB=2AD=2,∠BAD=60°,E为DC的中点,那么$\overrightarrow{AC}$与$\overrightarrow{EB}$所成角的余弦值为( )
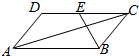

| A. | $\frac{\sqrt{7}}{7}$ | B. | -$\frac{\sqrt{7}}{7}$ | C. | $\frac{\sqrt{7}}{14}$ | D. | -$\frac{\sqrt{7}}{14}$ |
9.定义在R上的函数f(x)=$\frac{g(x)}{{2}^{x}}$,g(x)=g(2-x)•4x-1,若f(x)在[1,+∞)为增函数,则( )
| A. | g(1)>2g(0) | B. | g(3)>8g(0) | C. | g(2)>2g(0) | D. | g(4)<16g(0) |