题目内容
4.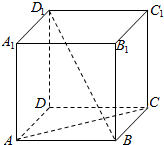 已知正方体ABCD-A1B1C1D1的棱长是a,用向量法证明AC⊥BD1.
已知正方体ABCD-A1B1C1D1的棱长是a,用向量法证明AC⊥BD1.
分析 如图所示,建立空间直角坐标系,只有证明$\overrightarrow{AC}$•$\overrightarrow{B{D}_{1}}$=0即可.
解答 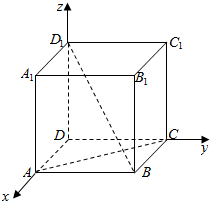 证明:如图所示,则A(a,0,0),B(a,a,0),C(0,a,0),D1(0,0,a),
证明:如图所示,则A(a,0,0),B(a,a,0),C(0,a,0),D1(0,0,a),
∴$\overrightarrow{AC}$=(-a,a,0),
$\overrightarrow{B{D}_{1}}$=(-a,-a,a),
∴$\overrightarrow{AC}$•$\overrightarrow{B{D}_{1}}$=a2-a2=0,
∴$\overrightarrow{AC}$⊥$\overrightarrow{B{D}_{1}}$,
∴AC⊥BD1.
点评 本题考查了向量数量积与向量垂直的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.若实数x,y满足$\left\{\begin{array}{l}{y≥2x-2}\\{y≥-x+1}\\{y≤x+1}\end{array}\right.$,则z=2x-y的最小值为( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
9.定义在R上的函数f(x)=$\frac{g(x)}{{2}^{x}}$,g(x)=g(2-x)•4x-1,若f(x)在[1,+∞)为增函数,则( )
| A. | g(1)>2g(0) | B. | g(3)>8g(0) | C. | g(2)>2g(0) | D. | g(4)<16g(0) |
14.将棱长为2的正四面体木块切削成一个体积最大的球,则该球的体积是( )
| A. | $\frac{\sqrt{6}π}{27}$ | B. | $\sqrt{6}$π | C. | $\frac{\sqrt{3}}{2}$π | D. | $\frac{4}{3}$π |