题目内容
16.某四棱锥的三视图如图所示,则该四棱锥的外接球的表面积是$\frac{353π}{16}$.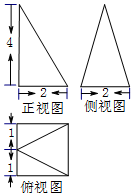
分析 由三视图知该四棱锥是如图所示的四棱锥S-ABCD,其中ABCD是边长为2的正方体,面SAD⊥面ABCD,SA=SD,AD中点为E,SE=4,由此求出外接球的半径,利用球体的表面积公式计算即可.
解答 解: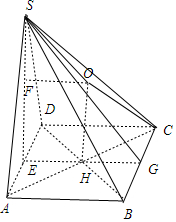 由三视图知该四棱锥是如图所示的四棱锥S-ABCD,
由三视图知该四棱锥是如图所示的四棱锥S-ABCD,
其中ABCD是边长为2的正方体,面SAD⊥面ABCD,SA=SD,
AD中点为E,SE=4,
其BC中点G,连结EG、SG,BD∩AC=H,
设该四棱锥的外接球球心为O,作OF⊥SE于F,
则OH⊥平面ABCD,OF=EH=1,CH=$\sqrt{2}$,
设OH=x,则SF=4-x,
∵OS=OC=R,
∴OS2=OC2,即(4-x)2+1=x2+2,解得x=$\frac{15}{8}$,
∴该四棱锥的外接球半径R=$\sqrt{(\frac{15}{8})^{2}+2}$=$\frac{\sqrt{353}}{8}$,
∴该四棱锥的外接球的表面积S=4πR2=4π×$\frac{353}{64}$=$\frac{353π}{16}$.
故答案为:$\frac{353π}{16}$.
点评 本题考查三视图求几何体的外接球的表面积的求法,考查空间想象能力、运算求解能力,考查数形结合思想、等价转化思想,是中档题.

练习册系列答案
相关题目
6.若点P(3,1)为圆(x-2)2+y2=16的弦AB的中点,则直线AB的方程为( )
| A. | x-3y=0 | B. | 2x-y-5=0 | C. | x+y-4=0 | D. | x-2y-1=0 |
4.已知某几何体的三视图如图所示,则该几何体的体积为( )
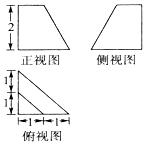

| A. | $\frac{7}{3}$ | B. | 7 | C. | 13 | D. | $\frac{{17+3\sqrt{10}}}{2}$ |
8.已知函数f(x)=3sin(2x-$\frac{π}{4}$),则下列结论正确的是( )
| A. | 若f(x1)=f(x2)=0,则x1-x2=kπ(k∈Z) | |
| B. | 函数f(x)的图象关于(-$\frac{π}{8}$,0)对称 | |
| C. | 函数f(x)的图象与g(x)=3cos(2x+$\frac{π}{4}$)的图象相同 | |
| D. | 函数f(x)在[-$\frac{1}{8}$π,$\frac{3}{8}$π]上递增 |
6.已知集合I={x∈Z|-3<x<3},A={-2,0,1},B={-1,0,1,2},则(∁IA)∩B等于( )
| A. | {-1} | B. | {2} | C. | {-1,2} | D. | {-1,0,1,2} |
 如图所示,在三棱柱ABC-A1B1C1中,四边形AA1B1B为边长为2的正方形,四边形BB1C1C为菱形,∠BB1C1=60°,平面AA1B1B⊥平面BB1C1C,点E、F分别是B1C,AA1的中点.
如图所示,在三棱柱ABC-A1B1C1中,四边形AA1B1B为边长为2的正方形,四边形BB1C1C为菱形,∠BB1C1=60°,平面AA1B1B⊥平面BB1C1C,点E、F分别是B1C,AA1的中点.