题目内容
设{an}是等比数列，若a2=3，a7=1，则数列{an}前8项的积为（ ）
| A、56 | B、80 | C、81 | D、128 |
考点：数列的求和,等比数列的前n项和,等比数列的性质
专题：等差数列与等比数列
分析：求出等比数列的公比，然后求解数列{an}前8项的积．
解答：
解：{an}是等比数列，若a2=3，a7=1，
∴1=3q5．q5=
．
数列{an}前8项的积为：a1•a2•a3…a8=a28q-1+0+1+2+3+4+5+6=38×（
）4=34=81．
故选：C．
∴1=3q5．q5=
| 1 |
| 3 |
数列{an}前8项的积为：a1•a2•a3…a8=a28q-1+0+1+2+3+4+5+6=38×（
| 1 |
| 3 |
故选：C．
点评：本题考查等比数列的基本性质的应用，数列求和的方法，整体代入的方法．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
在极坐标系中，点P是曲线C：ρ=2cosθ上的一点，则P的极坐标可能是（ ）
| A、（2，0） | ||
B、（2，
| ||
C、（1，
| ||
D、（1，
|
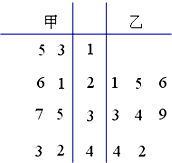以下茎叶图记录了甲、乙两名篮球运动员在以往几场比赛中得分的情况，设甲、乙两组数据的平均数分别为. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
四面体ABCD中，AD与BC互相垂直，AD=2BC=4，且AB+BD=AC+CD=2
，则四面体ABCD的体积的最大值是（ ）
| 14 |
| A、4 | ||
B、2
| ||
| C、5 | ||
D、
|
经过抛物线y=
x2的焦点和双曲线
-
=1的右焦点的直线方程为（ ）
| 1 |
| 4 |
| x2 |
| 17 |
| y2 |
| 8 |
| A、x+48y-3=0 |
| B、x+80y-5=0 |
| C、x+3y-3=0 |
| D、x+5y-5=0 |