题目内容
若直线(2a+b)x+y-1=0(a>0,b>0)经过椭圆
+
=1的右焦点,则
+
的最小值是( )
| x2 |
| 4 |
| y2 |
| 3 |
| 1 |
| a |
| 1 |
| b |
A、
| ||
| B、4 | ||
C、3+2
| ||
| D、6 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先求出椭圆的右焦点坐标,代入直线方程,求出2a+b的值,由此利用均值定理能求出结果.
解答:
解:∵直线(2a+b)x+y-1=0(a>0,b>0)经过椭圆
+
=1的右焦点,
∴2a+b=1,
∴
+
=(2a+b)(
+
)=3+
+
≥3+2
=3+2
.
∴
+
的最小值是3+2
.
故选:C.
| x2 |
| 4 |
| y2 |
| 3 |
∴2a+b=1,
∴
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| b |
| a |
| 2a |
| b |
|
| 2 |
∴
| 1 |
| a |
| 1 |
| b |
| 2 |
故选:C.
点评:本题考查椭圆的简单性质的应用,解题时要认真审题,注意均值定理的应用.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
下列求导运算正确的是( )
| A、(sinx)′=-cosx | ||||
| B、(cosx)′=sinx | ||||
C、(
| ||||
| D、(2x)′=x•2x-1 |
我们把离心率为黄金比
的椭圆称之为“优美椭圆”.设F1、F2是“优美椭圆”C:
+
=1(a>b>0)的左、右焦点,则椭圆C上满足∠F1PF2=90°的点P的个数为( )
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| A、0 | B、2 |
| C、4 | D、以上答案均不正确 |
用反证法证明命题:“a1,a2,a3,a4至少有一个数大于25”时,假设正确的是( )
| A、假设a1,a2,a3,a4都大于25 |
| B、假设a1,a2,a3,a4都小于或等于25 |
| C、假设a1,a2,a3,a4至多有一个数大于25 |
| D、假设a1,a2,a3,a4至少有两个数大于25 |
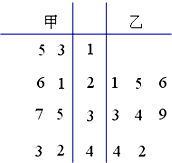 以下茎叶图记录了甲、乙两名篮球运动员在以往几场比赛中得分的情况,设甲、乙两组数据的平均数分别为
以下茎叶图记录了甲、乙两名篮球运动员在以往几场比赛中得分的情况,设甲、乙两组数据的平均数分别为. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
抛物线x2=(2a-1)y的准线方程为y=1,则实数a=( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
直线2ay-x=0与直线(3a-1)x-ay-1=0平行且不重合,则a等于( )
A、
| ||
B、
| ||
C、0或
| ||
D、0或
|
直线l1:(
-1)x+y-2=0与直线l2:(
+1)x-y-3=0的位置关系是( )
| 2 |
| 2 |
| A、平行 | B、相交 | C、垂直 | D、重合 |