题目内容
已知{an}为等比数列,a5+a8=2,a6•a7=-8,则a2+a11=( )
| A、5 | B、7 | C、-7 | D、-5 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:通过已知条件求出a5,a8,求出公比,求出a7,然后求解a2+a11的值.
解答:
解:a5+a8=2,a6•a7=-8,
∴a5•a8=-8,
解得a5=4,a8=-2,
或a5=-2,a8=4.
当a5=4,a8=-2,q3=-
,
a2+a11=a5q-3+a8q3=4×(
)-2×(-
)=-7,
当a5=-2,a8=4.q3=-2.
a2+a11=a5q-3+a8q3=-2×(-
)+4×(-2)=-7
故选:C.
∴a5•a8=-8,
解得a5=4,a8=-2,
或a5=-2,a8=4.
当a5=4,a8=-2,q3=-
| 1 |
| 2 |
a2+a11=a5q-3+a8q3=4×(
| 1 | ||
-
|
| 1 |
| 2 |
当a5=-2,a8=4.q3=-2.
a2+a11=a5q-3+a8q3=-2×(-
| 1 |
| 2 |
故选:C.
点评:本题考查等比数列的通项公式的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
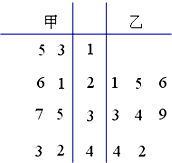 以下茎叶图记录了甲、乙两名篮球运动员在以往几场比赛中得分的情况,设甲、乙两组数据的平均数分别为
以下茎叶图记录了甲、乙两名篮球运动员在以往几场比赛中得分的情况,设甲、乙两组数据的平均数分别为. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
cos75°cos105°+sin75°sin105°的值是( )
| A、-1 | ||||
B、-
| ||||
C、
| ||||
D、
|
直线y=5,与y=-1在区间[0,
]上截曲线y=Asinωx+B(A>0,B>0,ω>0)所得弦长相等且不为零,则下列描述正确的是( )
| 2π |
| ω |
A、A≤
| ||||
| B、A≤3,B=2 | ||||
C、A>
| ||||
| D、A>3,B=2 |
直线l1:(
-1)x+y-2=0与直线l2:(
+1)x-y-3=0的位置关系是( )
| 2 |
| 2 |
| A、平行 | B、相交 | C、垂直 | D、重合 |
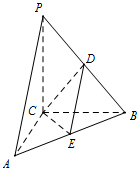 如图,在三棱锥P-ABC中,PB⊥AC,PC⊥平面ABC,点D,E分别为线段PB,AB的中点.
如图,在三棱锥P-ABC中,PB⊥AC,PC⊥平面ABC,点D,E分别为线段PB,AB的中点.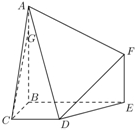 如图,多面体ABCDEF中,BA、BC、BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.
如图,多面体ABCDEF中,BA、BC、BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.