题目内容
下列函数是偶函数的是（ ）
| A、y=lgx2 | ||
B、y=（
| ||
| C、y=1-x2，x∈（-1，1] | ||
| D、y=x-1 |
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：根据函数奇偶性的定义和性质进行判断即可．
解答：
解：A．y=lgx2是偶函数，满足条件．
B．y=（
）x单调递减，为非奇非偶函数，不满足条件．
C．函数的定义域关于原点不对称，为非奇非偶函数，不满足条件．
D．y=x-1为奇函数，不满足条件．
故选：A．
B．y=（
| 1 |
| 2 |
C．函数的定义域关于原点不对称，为非奇非偶函数，不满足条件．
D．y=x-1为奇函数，不满足条件．
故选：A．
点评：本题主要考查函数奇偶性的判断，根据奇偶性的定义是解决本题的关键．
练习册系列答案
相关题目
我们把离心率为黄金比
的椭圆称之为“优美椭圆”．设F1、F2是“优美椭圆”C：
+
=1（a＞b＞0）的左、右焦点，则椭圆C上满足∠F1PF2=90°的点P的个数为（ ）
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| A、0 | B、2 |
| C、4 | D、以上答案均不正确 |
在极坐标系中，点P是曲线C：ρ=2cosθ上的一点，则P的极坐标可能是（ ）
| A、（2，0） | ||
B、（2，
| ||
C、（1，
| ||
D、（1，
|
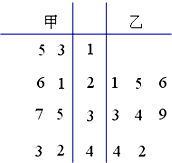以下茎叶图记录了甲、乙两名篮球运动员在以往几场比赛中得分的情况，设甲、乙两组数据的平均数分别为. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
经过抛物线y=
x2的焦点和双曲线
-
=1的右焦点的直线方程为（ ）
| 1 |
| 4 |
| x2 |
| 17 |
| y2 |
| 8 |
| A、x+48y-3=0 |
| B、x+80y-5=0 |
| C、x+3y-3=0 |
| D、x+5y-5=0 |
直线y=5，与y=-1在区间[0，
]上截曲线y=Asinωx+B（A＞0，B＞0，ω＞0）所得弦长相等且不为零，则下列描述正确的是（ ）
| 2π |
| ω |
A、A≤
| ||||
| B、A≤3，B=2 | ||||
C、A＞
| ||||
| D、A＞3，B=2 |