题目内容
已知函数f(x)=lgkx,g(x)=lg(x+1).
(Ⅰ)当k=1时,求函数y=f(x)+g(x)的单调区间;
(Ⅱ)若方程f(x)=2g(x)仅有一个实根,求实数k的取值集合.
(Ⅰ)当k=1时,求函数y=f(x)+g(x)的单调区间;
(Ⅱ)若方程f(x)=2g(x)仅有一个实根,求实数k的取值集合.
考点:函数的最值及其几何意义,函数单调性的判断与证明
专题:函数的性质及应用
分析:本题(Ⅰ)利用k=1对f(x)+g(x)进行化简,然后根据复合函数的单调性规律,求出函数的单调区间;(Ⅱ)将方程f(x)=2g(x)等价转化为普通的一元二次不等式,然后对一元二次不等式的解进行研究,得到本题的答案.
解答:
解:(Ⅰ)当k=1时,y=f(x)+g(x)=lgx+lg(x+1)=lg[x(x+1)](其中x>0)
∵y=x(x+1)在(0,+∞)单调递增,且值域为(0,+∞),
∴y=f(x)+g(x)的单调递增区间为(0,+∞),不存在单调递减区间.
(Ⅱ)由f(x)=2g(x),即lgkx=2lg(x+1).该方程可化为不等式组
,
①若k>0时,则x>0,原问题即为:方程kx=(x+1)2在(0,+∞)上有且仅有一个根,
即x2+(2-k)x+1=0在(0,+∞)上有且仅有一个根,
由x1•x2=1>0知:△=0.
解得k=4;
②若k<0时,则-1<x<0,原问题即为:方程kx=(x+1)2在(-1,0)上有且仅有一个根,
即x2+(2-k)x+1=0在(-1,0)上有且仅有一个根,
记h(x)=x2+(2-k)x+1,
由f(0)=1>0知:f(-1)<0,
解得k<0.
综上可得k<0或k=4.
∴实数k的取值集合为{k|k<0或k=4}.
∵y=x(x+1)在(0,+∞)单调递增,且值域为(0,+∞),
∴y=f(x)+g(x)的单调递增区间为(0,+∞),不存在单调递减区间.
(Ⅱ)由f(x)=2g(x),即lgkx=2lg(x+1).该方程可化为不等式组
|
①若k>0时,则x>0,原问题即为:方程kx=(x+1)2在(0,+∞)上有且仅有一个根,
即x2+(2-k)x+1=0在(0,+∞)上有且仅有一个根,
由x1•x2=1>0知:△=0.
解得k=4;
②若k<0时,则-1<x<0,原问题即为:方程kx=(x+1)2在(-1,0)上有且仅有一个根,
即x2+(2-k)x+1=0在(-1,0)上有且仅有一个根,
记h(x)=x2+(2-k)x+1,
由f(0)=1>0知:f(-1)<0,
解得k<0.
综上可得k<0或k=4.
∴实数k的取值集合为{k|k<0或k=4}.
点评:本题考查的是复合函数单调性、函数的定义域、一元二次函数的图象和性质,还考查了分类讨论的数学思想.本题有一定的综合性,对学生能力要求较高,属于中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
下列命题正确的是( )
| A、小于90°的角一定是锐角 | ||
| B、终边相同的角一定相等 | ||
C、终边落在直线y=
| ||
| D、α-β=kπ,k∈Z,则角α的正切值等于角β的正切值 |
正方体ABCD-A1B1C1D1中,M,N分别为AB,DC中点,则直线MC与D1N所成角的余弦值为( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
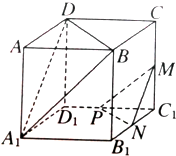 在如图所示的正方体ABCD-A1B1C1D1中.
在如图所示的正方体ABCD-A1B1C1D1中.