题目内容
△ABC中，角A，B，C的对边分别是a，b，c且满足（2a-c）cosB=bcosC，
（1）求角B的大小；
（2）若△ABC的面积为
且b=
，求a+c的值．
（1）求角B的大小；
（2）若△ABC的面积为
3
| ||
| 4 |
| 3 |
考点：正弦定理的应用,余弦定理
专题：解三角形
分析：（1）结合三角形的内角和定理及诱导公式可得sin（C+B）=sinA，再对已知（2a-c）cosB=bcosC，利用正弦定理化简可求B
（2）结合三角形的面积公式S=
acsinB，可求ac，由已知b，B，再利用余弦定理b2=a2+c2-2accosB可求a+c
（2）结合三角形的面积公式S=
| 1 |
| 2 |
解答：
解：（1）又A+B+C=π，即C+B=π-A，
∴sin（C+B）=sin（π-A）=sinA，
将（2a-c）cosB=bcosC，利用正弦定理化简得：（2sinA-sinC）cosB=sinBcosC，
∴2sinAcosB=sinCcosB+sinBcosC=sin（C+B）=sinA，
在△ABC中，0＜A＜π，sinA＞0，∴cosB=
，又0＜B＜π，则B=
（2）∵△ABC的面积为
，sinB=sin
=
，
∴S=
acsinB=
ac=
，∴ac=3，又b=
，cosB=cos
=
，
∴由余弦定理b2=a2+c2-2accosB得：a2+c2-ac=（a+c）2-3ac=（a+c）2-9=3，
∴（a+c）2=12，则a+c=2
∴sin（C+B）=sin（π-A）=sinA，
将（2a-c）cosB=bcosC，利用正弦定理化简得：（2sinA-sinC）cosB=sinBcosC，
∴2sinAcosB=sinCcosB+sinBcosC=sin（C+B）=sinA，
在△ABC中，0＜A＜π，sinA＞0，∴cosB=
| 1 |
| 2 |
| π |
| 3 |
（2）∵△ABC的面积为
3
| ||
| 4 |
| π |
| 3 |
| ||
| 2 |
∴S=
| 1 |
| 2 |
| ||
| 4 |
3
| ||
| 4 |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
∴由余弦定理b2=a2+c2-2accosB得：a2+c2-ac=（a+c）2-3ac=（a+c）2-9=3，
∴（a+c）2=12，则a+c=2
| 3 |
点评：本题主要考查了正弦定理、余弦定理在求解三角形中的应用，解决此类问题的关键是要是考生具备综合应用公式的能力
练习册系列答案
相关题目
为了得到函数y=cos（x+
）的图象，只需把余弦曲线y=cosx上的所有的点（ ）
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
在△ABC中，若最大角的正弦值是
，则△ABC必是（ ）
| ||
| 2 |
| A、等边三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、锐角三角形 |
如图，在几何体ABC-A1B1C1中，点A1，B1，C1在平面ABC内的正投影分别为A，B，C，且AB⊥BC，E为AB1中点，AB=AA1=BB1=2CC1．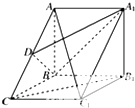
如图所示，在三棱柱ABC-A1B1C1中，侧面A1ABB1和BCC1B1是两个全等的正方形，AC1⊥平面A1DB，D为AC的中点．