题目内容
在△ABC中，a，b，c成等比数列，
（1）若B是A和C的等差中项，求A；
（2）若b=1，求△ABC的面积的最大值．
（1）若B是A和C的等差中项，求A；
（2）若b=1，求△ABC的面积的最大值．
考点：余弦定理
专题：等差数列与等比数列,解三角形
分析：（1）利用等差数列与等比数列的定义、余弦定理、等边三角形的性质即可得出；
（2）利用余弦定理、基本不等式、正弦函数的单调性、三角形的面积计算公式即可得出．
（2）利用余弦定理、基本不等式、正弦函数的单调性、三角形的面积计算公式即可得出．
解答：
解：（1）∵2B=A+C，且A+B+C=180°，∴B=60°．
又b2=a2+c2-2accos60°=a2+c2-ac，且b2=ac，
∴（a-c）2=0
∴a=c，
故A=60°．
（2）∵cosB=
≥
=
=
，
∴0＜B≤
，进而0＜sinB≤
．
∴S△=
acsinB≤
×12×
=
．
∴（S△ABC）max=
．
又b2=a2+c2-2accos60°=a2+c2-ac，且b2=ac，
∴（a-c）2=0
∴a=c，
故A=60°．
（2）∵cosB=
| a2+c2-b2 |
| 2ac |
| 2ac-b2 |
| 2ac |
| 2ac-ac |
| 2ac |
| 1 |
| 2 |
∴0＜B≤
| π |
| 3 |
| ||
| 2 |
∴S△=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
∴（S△ABC）max=
| ||
| 4 |
点评：本题考查了等差数列与等比数列的定义、余弦定理、等边三角形的性质、基本不等式、正弦函数的单调性、三角形的面积计算公式等基础知识与基本技能方法，考查了推理能力和计算能力，属于中档题．
练习册系列答案
相关题目
已知α∈R，sin2α+4sinαcosα+4cos2α=
，则tanα=（ ）
| 5 |
| 2 |
| A、3 | ||
B、
| ||
C、3或-
| ||
D、-3或
|
如图，在几何体ABC-A1B1C1中，点A1，B1，C1在平面ABC内的正投影分别为A，B，C，且AB⊥BC，E为AB1中点，AB=AA1=BB1=2CC1．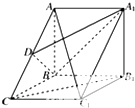
如图所示，在三棱柱ABC-A1B1C1中，侧面A1ABB1和BCC1B1是两个全等的正方形，AC1⊥平面A1DB，D为AC的中点．