题目内容
2.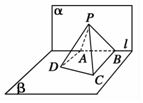 如图,已知平面α⊥β,α∩β=l,A,B是直线l上的两点,C,D是平面β内的两点,且 DA⊥l,CB⊥l,DA=2,AB=4,CB=4,P是平面α上的一动点,且直线 PD,PC与平面α所成角相等,则二面角 P-BC-D的余弦值的最小值是$\frac{\sqrt{3}}{2}$.
如图,已知平面α⊥β,α∩β=l,A,B是直线l上的两点,C,D是平面β内的两点,且 DA⊥l,CB⊥l,DA=2,AB=4,CB=4,P是平面α上的一动点,且直线 PD,PC与平面α所成角相等,则二面角 P-BC-D的余弦值的最小值是$\frac{\sqrt{3}}{2}$.
分析 ∠PBA为所求的二面角的平面角,由△DAP∽△CPB得出$\frac{PA}{PB}=\frac{DA}{BC}$=$\frac{1}{2}$,求出P在α内的轨迹,根据轨迹的特点求出∠PBA的最大值对应的余弦值.
解答  解:∵AD⊥l,α∩β=l,α⊥β,AD?β,
解:∵AD⊥l,α∩β=l,α⊥β,AD?β,
∴AD⊥α,同理:BC⊥α.
∴∠DPA为直线PD与平面α所成的角,
∠CPB为直线PC与平面α所成的角,
∴∠DPA=∠CPB,又∠DAP=∠CBP=90°
∴△DAP∽△CPB,
∴$\frac{PA}{PB}=\frac{DA}{BC}$=$\frac{1}{2}$.
在平面α内,以AB为x轴,以AB的中垂线为y轴建立平面直角坐标系,
则A(-2,0),B(2,0).设P(x,y),(y>0)
∴2$\sqrt{(x+2)^{2}+{y}^{2}}$=$\sqrt{(x-2)^{2}+{y}^{2}}$,整理得(x+$\frac{10}{3}$)2+y2=$\frac{64}{9}$,
∴P点在平面α内的轨迹为以M(-$\frac{10}{3}$,0)为圆心,以$\frac{8}{3}$为半径的上半圆.
∵平面PBC∩平面β=BC,PB⊥BC,AB⊥BC,
∴∠PBA为二面角P-BC-D的平面角.
∴当PB与圆相切时,∠PBA最大,cos∠PBA取得最小值.
此时PM=$\frac{8}{3}$,MB=$\frac{16}{3}$,MP⊥PB,∴PB=$\frac{8\sqrt{3}}{3}$.
cos∠PBA=$\frac{PB}{MB}$=$\frac{\sqrt{3}}{2}$.
故答案为$\frac{\sqrt{3}}{2}$.
点评 本题考查二面角的余弦值的最小值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案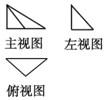 一个高为2的三棱锥的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,则该几何体外接球的体积( )
一个高为2的三棱锥的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,则该几何体外接球的体积( )| A. | 12π | B. | 9π | C. | $4\sqrt{3}π$ | D. | $\sqrt{3}π$ |
| A. | {x|0<x<1} | B. | {x|1<x<2} | C. | {x|-1<x<0} | D. | {x|-1<x<2} |
| A. | a<c<b | B. | a<b<c | C. | c<b<a | D. | b<c<a |
 某次比赛甲得分的茎叶图如图所示,若去掉一个最高分,去掉一个最低分,则剩下4个分数的方差为14.
某次比赛甲得分的茎叶图如图所示,若去掉一个最高分,去掉一个最低分,则剩下4个分数的方差为14.