题目内容
7．已知集合A={x|0＜x＜2}，B={x|x2-1＞0}，那么A∩B=（ ）| A． | {x|0＜x＜1} | B． | {x|1＜x＜2} | C． | {x|-1＜x＜0} | D． | {x|-1＜x＜2} |
分析 求出B中不等式的解集确定出B，找出A与B的交集即可．
解答 解：由B中不等式变形得：（x+1）（x-1）＞0，
解得：x＜-1或x＞1，即B={x|x＜-1或x＞1}，
∵A={x|0＜x＜2}，
∴A∩B={x|1＜x＜2}，
故选：B．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
17．下列四个函数中，在其定义域上既是奇函数又是单调递增函数的是（ ）
| A． | y=ex | B． | y=log2x | C． | y=sinx | D． | y=x3 |
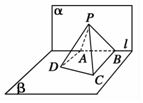如图，已知平面α⊥β，α∩β=l，A，B是直线l上的两点，C，D是平面β内的两点，且 DA⊥l，CB⊥l，DA=2，AB=4，CB=4，P是平面α上的一动点，且直线 PD，PC与平面α所成角相等，则二面角 P-BC-D的余弦值的最小值是$\frac{\sqrt{3}}{2}$．
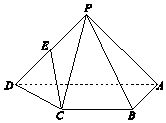如图，在四棱锥P-ABCD中，AD∥BC，∠BAD=90°，PA=PD，AB⊥PA，AD=2，AB=BC=1
16．已知集合A={x|$\sqrt{2x-1}$＞1}，则∁RA=（ ）
| A． | {x|x＞1} | B． | {x|x≥$\frac{1}{2}$} | C． | {x|x≤1} | D． | {x|x＜$\frac{1}{2}$} |
16．与直线 $y=\frac{1}{2}x+1$垂直，且过（2，0）点的直线方程是（ ）
| A． | y=-2x+4 | B． | $y=\frac{1}{2}x-1$ | C． | y=-2x-4 | D． | $y=\frac{1}{2}x-4$ |