题目内容
17．
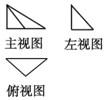一个高为2的三棱锥的三视图如图所示，其中俯视图是一个腰长为2的等腰直角三角形，则该几何体外接球的体积（ ）| A． | 12π | B． | 9π | C． | $4\sqrt{3}π$ | D． | $\sqrt{3}π$ |
分析 PC的中点为O，连接OA，OB，运用线面垂直的判断和性质，证得BC⊥PB，可得O为球心，求出半径，即可得到体积．
解答 
解：一个高为2的三棱锥P-ABC，如图所示，
PC的中点为O，连接OA，OB，
由PA⊥底面ABC，可得PA⊥BC，
AB⊥BC，
可得BC⊥平面PAB，
即有BC⊥PB，
可得OA=OB=OC=OP，
即O为球心，半径为$\sqrt{3}$，
则球的体积为V=$\frac{4}{3}$π•（$\sqrt{3}$）3=4$\sqrt{3}$π．
故选：C．
点评 本题考查三棱锥的外接球的体积，注意将三视图转化为直观图，确定球心是解题的关键，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
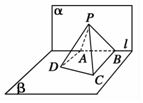如图，已知平面α⊥β，α∩β=l，A，B是直线l上的两点，C，D是平面β内的两点，且 DA⊥l，CB⊥l，DA=2，AB=4，CB=4，P是平面α上的一动点，且直线 PD，PC与平面α所成角相等，则二面角 P-BC-D的余弦值的最小值是$\frac{\sqrt{3}}{2}$．
如图，在半径为30cm的半圆形铁皮上截取一块矩形材料ABCD（点A，B在直径上，点C，D在半圆周上），并将其卷成一个以AD为母线的圆柱体罐子的侧面（不计剪裁和拼接损耗）．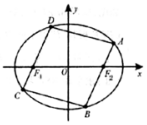
已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的短轴的一个顶点与两个焦点构成正三角形，且该三角形的周长为6