题目内容
在区间[0,1]上随机取三个数x,y,z,事件A={(x,y,z)|x2+y2+z2<1},则P(A)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:在区间[0,1]上随机取三个数x,y,z,则点(x,y,z)在棱长为1的正方体内,其体积V=13.x2+y2+z2<1表示的是以原点(0,0,0)为球心,1为半径的球内的点.而事件A={(x,y,z)|x2+y2+z2<1}中的点表示的是球在正方体内部的点,利用球的体积计算公式可得出.再利用几何概型的计算公式即可得出.
解答:
解:在区间[0,1]上随机取三个数x,y,z,
则点(x,y,z)在棱长为1的正方体内,其体积V=13=1.
x2+y2+z2<1表示的是以原点(0,0,0)为球心,1为半径的球内的点.
而事件A={(x,y,z)|x2+y2+z2<1}中的点表示的是球在正方体内部的点,
因此P(A)=
=
.
故选:C.
则点(x,y,z)在棱长为1的正方体内,其体积V=13=1.
x2+y2+z2<1表示的是以原点(0,0,0)为球心,1为半径的球内的点.
而事件A={(x,y,z)|x2+y2+z2<1}中的点表示的是球在正方体内部的点,
因此P(A)=
| ||||
| 1 |
| π |
| 6 |
故选:C.
点评:本题考查了几何概型的计算,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
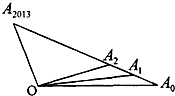 如图,O为线段A0A2013外一点,若A0,A1,A2,A3,…,A2013中任意相邻两点的距离相等,
如图,O为线段A0A2013外一点,若A0,A1,A2,A3,…,A2013中任意相邻两点的距离相等,| OA0 |
| a |
| OA2013 |
| b |
| a |
| b |
| OA0 |
| OA1 |
| OA2 |
| OA2013 |
A、1006(
| ||||
B、1007(
| ||||
C、2012(
| ||||
D、2014(
|
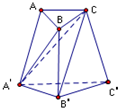 如图所示,三棱台ABC-A′B′C′中,AB:A′B′=1:2,则三棱锥C-A′B′C′,B-A′B′C,A′-ABC的体积之比为( )
如图所示,三棱台ABC-A′B′C′中,AB:A′B′=1:2,则三棱锥C-A′B′C′,B-A′B′C,A′-ABC的体积之比为( )| A、1:1:1 |
| B、2:1:1 |
| C、4:2:1 |
| D、4:4:1 |
圆柱的一个底面积为S,侧面展开图是一个正方形,那么这个圆柱的体积是( )
A、
| ||||
B、
| ||||
C、2S
| ||||
D、S
|
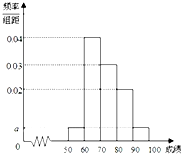 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].